[阅读笔记] 均匀分布随机数之和
[0, 1] 闭区间上的独立同分布的均匀随机变量分布求和(Uniform Sum Distribution),项数n越多,也接近正态分布。对于大多数实际应用,3项就基本上满足正态分布了。
有趣的结果,意想不到的用途!!
一、n项独立同分布的均匀随机变量分布求和的概率密度公式
《Encyclopedia of Mathematics》里的3项均匀分布求和的概率密度公式:
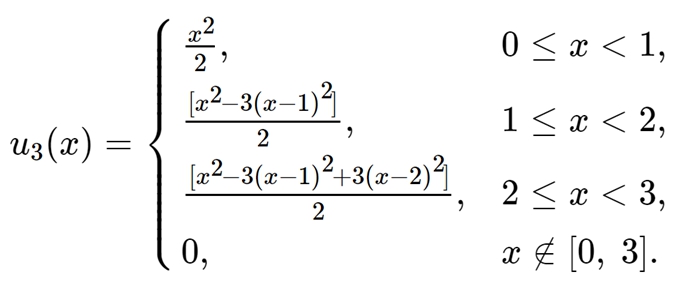
https://encyclopediaofmath.org/wiki/Uniform_distribution
n项均匀分布求和的概率密度公式:

https://encyclopediaofmath.org/wiki/Uniform_distribution
当项数 n → ∞ 时,趋向于均值为(n/2)、方差为(n/12)的正态分布。
二、n项独立同分布的均匀随机变量分布求和的概率密度的图示
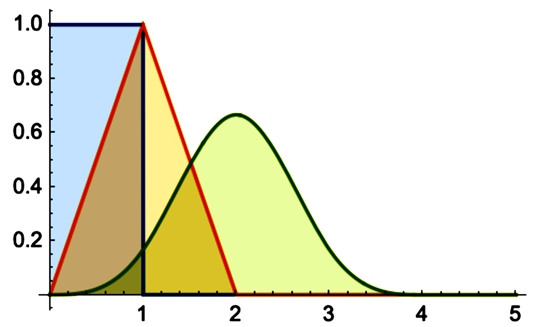
WOLFRAM 均匀分布求和:项数n = 1、2、4。

WOLFRAM 均匀分布求和:项数n = 4、8、16。
https://reference.wolfram.com/language/ref/UniformSumDistribution.html
感谢 Encyclopedia of Mathematics 和 Wolfram 网站的重要资料!
祝福您们!
参考资料:
[1] Uniform distribution. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Uniform_distribution
[2] Uniform Sum Distribution -- from Wolfram MathWorld
https://mathworld.wolfram.com/UniformSumDistribution.html
[3] UniformSumDistribution—Wolfram Language Documentation, Wolfram Research (2010),UniformSumDistribution,Wolfram 语言函数,(更新于 2016 年).
https://reference.wolfram.com/language/ref/UniformSumDistribution.html
相关链接:
[1] 2021-7-22,[重大困惑] 为什么正态分布随机数不能“被”预测
http://blog.sciencenet.cn/blog-107667-1296529.html
[2] 2020-03-26,现实中常见的概率分布
http://blog.sciencenet.cn/blog-107667-1225390.html
感谢您的指教!
感谢您指正以上任何错误!
感谢您提供更多的相关资料!

转载本文请联系原作者获取授权,同时请注明本文来自杨正瓴科学网博客。
链接地址:https://m.sciencenet.cn/blog-107667-1296695.html?mobile=1
收藏


