“∑(μ_i·dn_i)”是平衡态热力学教学中出现频率较高的一物理量. 本文拟结合具体的热力学过程，介绍“∑(μ_i·dn_i)”的热力学内涵.

        “∑(μ_i·dn_i)”是典型的热力学过程量，不同的热力学过程，其含义有差别.

 1. 气体的pVT变化

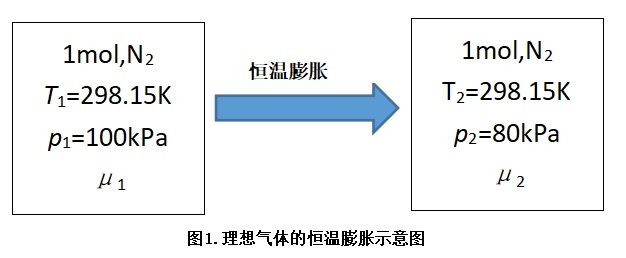
 例1. 298.15K、100kPa下1摩尔氮气，恒温条件下膨胀至80kPa，计算该过程的ΔG.

 解：对应的热力学过程参见如下图1.

       由热力学基本方程可得^[1]：dG=-S·dT+V·dp+δW'                  （1）

       依题：该过程恒温及有效功为0，即：dT=0， δW' =0.

       将上述条件代入式（1）可得：dG=V·dp                              （2）

       另：ΔG=∫∑(μ_i·dn_i)=μ₂×+μ₁×

                   =μ₂×1mol-μ₁×1mol=μ₂-μ₁          （3）

       结合式（2）与（3）可得：

         ΔG=μ₂-μ₁ =∫（n·RT/p）·dp                                     （4）

       整理式（4）可得：ΔG=μ₂-μ₁ =n·RT·ln(p₂/p₁)            （5）

       将已知条件代入式（5）可得：

          ΔG=μ₂-μ₁ =1mol×8.315J·mol^-1·K^-1×298.15K×ln(100kPa/80kPa)

               =553.20J

       由上可得：理想气体的pVT变化中，∑(μ_i·dn_i)的积分结果，等于系统终态的吉布斯能减去系统始态的吉布斯能，即： ΔG=G₂-G₁=∫∑(μ_i·dn_i)=μ₂-μ₁，与热力学过程是否恒压无关.

 2. 相变

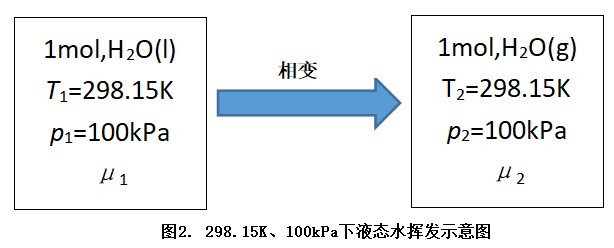
 例2. 298.15K、100kPa下1摩尔液态水挥发为水蒸气，计算该过程的Δ_rG^θ_m.

 解：对应的热力学过程参见如下图2.

       由热力学基本方程可得：dG=-S·dT+V·dp+δW'                  （1）

       依题：该过程恒温、恒压及环境不提供有效功，即：dT=0，dp=0, δW_e'=0*.

       *备注：δW'=δW_e'+δW_s'        （6）

          式（6）中δW_e'代表环境提供系统的有效功；δW_s'代表系统自身产生的有效功. 

          依题δW_e'=0, δW'=δW_s'

       将上述条件代入式（1）可得：dG=δW'=δW_s'                               （7） 

        Δ_rG^θ_m=∫∑(μ_i·dn_i)=μ₂×+μ₁×

                  =μ₂×1mol-μ₁×1mol=μ₂-μ₁          （8）

       另由热力学基本原理可得^[2]：

        Δ_rG^θ_m=∑（ν_i·Δ_fG^θ_m,i）=Δ_fG^θ_m(H₂O，g)-Δ_fG^θ_m(H₂O，l)

                   =-228.572kJ·mol^-1-(-237.129)kJ·mol^-1

                   =8.557kJ·mol^-1>0

       计算结果表明，298.15K、100kPa下1摩尔液态水挥发为水蒸气为非自发过程.

       由上可得：相变中，∑(μ_i·dn_i)的积分结果，等于系统终态的吉布斯能减去系统始态的吉布斯能，即：∫∑(μ_i·dn_i)=G₂-G₁.

 3. 化学反应

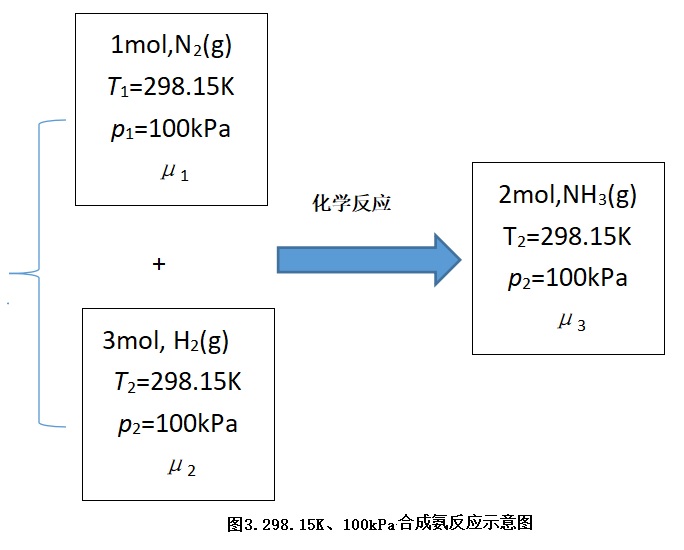
例3. 298.15K、100kPa下化学反应N₂(g)+3H₂(g)=2NH₃(g)，计算该过程的Δ_rG^θ_m.

 解：对应的热力学过程参见如下图3.

       由热力学基本方程可得：dG=-S·dT+V·dp+δW'                  （1）

       依题：该过程恒温、恒压及环境不提供有效功，即：dT=0，dp=0, δW_e'=0.

       将上述条件代入式（1）可得：dG=δW'=δW_s'                               （9） 

       Δ_rG^θ_m=∫∑(μ_i·dn_i)=μ₃×+μ₁×+μ₂×

                  =μ₃×2mol-μ₁×1mol-μ₂×3mol=2μ₃-3μ₂-μ₁          （10）

       另由热力学基本原理可得：

        Δ_rG^θ_m=∑（ν_i·Δ_fG^θ_m,i）=2Δ_fG^θ_m(NH₃，g)-3Δ_fG^θ_m(H₂，g)-Δ_fG^θ_m(N₂，g)

                  =2mol×(-16.45)kJ·mol^-1

                  =-32.90kJ·mol^-1<0

      计算结果表明，298.15K、100kPa下合成氨的反应为自发过程.

      由上可得：合成氨的化学反应中，∑(μ_i·dn_i)的积分结果，等于系统终态的吉布斯能减去系统始态的吉布斯能，即：∫∑(μ_i·dn_i)=G₂-G₁.

4.结论

  ⑴∑(μ_i·dn_i)的积分结果，等于系统终态的吉布斯能减去系统始态的吉布斯能   

  ⑵ 由气体pVT变化讨论可知：dG=∑(μ_i·dn_i)=-S·dT+V·dp+δW' 较dG=-S·dT+V·dp+∑(μ_i·dn_i)更合理.

 参考文献

[1]余高奇. 热力学第一定律研究.http://blog.sciencenet.cn/u/yugaoqi666 .科学网博客, 2021,8.

[2] Lide D R. CRC Handbook of Chemistry and Physics. 89th ed, Chemical Co, 2008,17:2688.