本文拟在“混合过程的熵变计算探究”的基础上^[1]，结合具体实例，进一步探讨理想液态混合物混合过程

dG=∑μ_idn_i=-SdT+Vdp+δW' 的积分式，并给出 现象的一种可能解释.

        [例1] 25℃下，由各为0.5mol的纯溶剂A与B混合形成理想液态混合物，试计算该混合过程Δ_mixG与Δ_mixS .

 1. dG积分式的探讨

        dG=∑μ_idn_i=-SdT+Vdp+δW'            （1）

        式（1）是理想液态混合物混合过程最重要的热力学基本方程式之一. 

        理想液态混合物混合条件为：①恒温（或dT=0)；②δW'=0（因没有化学反应或相变发生）.

        将上述两条件代入式（1）可得：

          dG=∑μ_idn_i=Vdp            （2）

        另理想液态混合物中任一组分B的化学势可表示为： μ_B= μ_B^*+RT·lnx_B        （3）

        式（2）积分，并结合式（3）可得：

                                   Δ_mixG=G_终态-G_始态                   

                                                    =[0.5mol×(μ_A^*+RT·lnx_A)+0.5mol×(μ_B^*+RT·lnx_B)]-(0.5mol×μ_A^*+0.5mol×μ_B^*)

                                             =0.5mol×RT·lnx_A+0.5mol×RT·lnx_B                    （4）

        依例1，x_A=x_B=0.5mol/(0.5mol+0.5mol)=0.5                                         （5）

        将式（5）代入式（4）可得：

        Δ_mixG=0.5mol×8.314J·K^-1·mol^-1×298.15K×ln0.5+0.5mol×8.314J·K^-1·mol^-1×298.15K×ln0.5

                  = -1.7182kJ·mol^-1                                                                           （6）

      另：                                                        （7）

     将式（6）结果代入式（7）可得：

       （8）

    整理式（8）可得：Δ_mixS= 5.7628J·K^-1·mol^-1

 2. 溶剂压与Vdp的积分式探讨

     为解释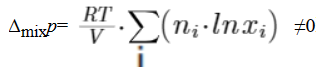现象，特引入溶剂压（Π）及溶剂压常数（k）.

  2.1 溶剂压（Π）

        同气体分子不停碰撞容器壁并产生压强一样，溶剂分子也产生溶剂压（Π）.

        溶剂压定义参见如下式（9）.

         Π=nRT/ V       （9）

        式（9）中，Π代表溶剂压，单位为Pa；n表示溶剂的物质的量，单位为mol；R表示摩尔理想溶剂常数，

R=8.314J·K^-1·mol^-1；T为体系温度，单位为K；V代表溶剂总体积，单位为m³.

        另理想液态混合物中任一i组分的溶剂压：Π_i=n_i·RT/ V       （10）

        不同溶剂混合时，溶剂压将发生作用，需消耗能量；可表示为：

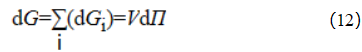
         由式（9）可得：       

        将式（13）代入式（12），并积分可得：                                    

        由式（14）可得：Δ_mixG_i=n_i·RT ·ln(Π_终态/Π_始态)                                                                 （15）

  2.2 溶剂压常数（k）

        通常情况下，某溶剂（i）的溶剂压（Π_i）与理想液态混合物中该溶剂的物质的量分数（x_i）成正比；参

见如下式（16）：   Π_i=k_i·x_i                   （16）

        式（16）中k_i称溶剂压常数，k_i与温度及溶剂i的性质有关，与溶剂体积及理想液态混合物中其它溶剂无

关. k_i的单位为Pa.

        另需指出：溶剂压常数（k_i）也可解读为一定温度时，某i纯溶剂所拥有的溶剂压.

        则：Π_终态,i=k_i·x_i                     （17）

               Π_始态,i=k_i                          （18） 

        将式（17）及（18）代入式（14）可得：

           Δ_mixG=∑(Δ_mixG_i)=RT·∑(n_i ·lnx_i)             （19）

        由式（19）可得：Δ_mixG_i=n_i ·RT·lnx_i       （20）

3.结论

     ⑴Π=nRT/ V ，Π_i=n_i·RT/ V；

      ⑵Π_i=k_i·x_i ；

      ⑶ Δ_mixG=∑(Δ_mixG_i)，Δ_mixG_i=n_i ·RT·lnx_i  .

参考文献

[1]余高奇.混合过程的熵变计算探究.http://blog.sciencenet.cn/u/yugaoqi666. 科学网博客, 2023,2.