博文
临床研究常用统计方法
|
统计分析贯穿于临床研究之中,在研究开始之初,就需要根据研究目的计算样本量。这一点在随机临床试验中尤为重要,如果纳入样本量大于所需样本量,浪费人力物力财力,尤其不符合伦理准则。如果纳入样本量小于所需样本量,统计分析时把握度(Power of test)太低,得不到有效结论。数据收集之后,治疗干预措施等是否有效也需要深入的统计分析才能得到答案。因此,统计分析是临床研究的重要组成部分。
1. 基线资料比较
临床研究病人一般是分成研究组(处理)和对照组,有时候也会有多个研究(处理)组。这些组别间患者的基线资料比较所用统计学方法和基础研究常用统计分析方法差不多,两组之间的比较用t检验、Wilcoxon秩和检验、卡方检验或费舍尔精确检验;多组之间的比较用方差分析,Kruskal-Wallis检验和卡方检验。(实例3.5)
实例3.5 研究者开展一项横断面调查研究分析肝癌的危险因素,收集病人的年龄、性别、身高、体重、是否HBV感染、是否HCV感染、是否酗酒(分为极少、偶尔[一月100 ml相当于50度的白酒]、经常[一周100 ml相当于50度的白酒]、频繁[一天100 ml相当于50度的白酒])、直系亲属是否有人患肝癌等信息,分析肝癌和非肝癌人群这些基本信息是否有差异? 研究对象的年龄、身高、体重等是数据变量,一般是正态分布,如果方差齐性,比较用t检验;两组研究对象在酗酒之间的差异按调查算是等级变量,采用Wilcoxon秩和检验;研究对象性别、是否病毒感染及直系亲属是否有人患肝癌是二分类变量,可以使用卡方检验。 如果研究者想将研究人群细化为正常、肝纤维化、肝硬化、肝癌组来分析,此时就是多组的分析比较了,研究对象的年龄、身高、体重等是一般是正态分布的数据变量,如果方差齐性,可以使用方差分析,如果有差异,进一步使用Post hoc分析究竟是哪两组之间有差异。多组之间的酗酒情况使用Kruskal-Wallis检验;而多组之间病毒感染及直系亲属遗传情况使用卡方分析。 |
2. 相关性分析和回归分析
临床研究中患者的某些生化指标或疾病其他指标之间可能会具有一定的相关性,如何确定两组数据之间是否具有相关性呢?可以使用如下相关性分析工具。如果两组都是连续性数据,可以使用Pearson相关分析,等级数据则使用Spearmen等级相关分析。相关分析会得到一个相关系数r和显著性差异P值,在对分析结果进行解释时除了看P值,还要看r值和样本量。即使P值小于0.05,在样本量和r绝对值比较小的时候也需要谨慎解释。
回归分析(Regression analysis)和相关性分析使用的方法是一样的,不同之处在于对分析结果的解释。相关性分析分析的两组变量是平等的,不存在因果关系,一般用于横断面研究或其他无法确定因果关系的研究。回归分析是由因及果的过程,两个变量是因果关系,多用于有时间轴向、事情发生有明显先后顺序的研究。如果是分析多个变量和一个变量的因果关系,那就是多元回归分析(Multiple regression analysis)。
有一种特殊的回归分析被广泛应用于临床医学统计,那就是Logistic回归分析(Logistic regression),它的结局只有两种情况(生死、有无、好坏等),是多元回归分析的一种特殊情况,常用于疾病危险因素分析。
相关分析例子见实例3.6。
实例3.6 研究者想研究乙肝患者肝脏病理分级和血清ALT水平是否相关,血清HBV表面抗原水平是否和血清ALT水平相关,应如何分析? 肝脏病理分级是等级资料,所以用Spearmen等级相关分析;而血清HBV表面抗原和血清ALT都是数据变量,先将HBV表面抗原水平对数转换后,再用Pearson相关分析。 |
3. 接收者操作特征曲线(又称受试者工作特征曲线,Receiver operating characteristic curve, ROC曲线)
临床诊断性实验的质量通常用敏感度和特异度来衡量。在同一研究中,如果取不同的临界值,则可得到不同的敏感度和特异度,将这些点在以敏感度为Y轴,以(1-特异度) 为X轴的坐标上标出并连成线,就可得到一条ROC曲线。ROC曲线是临床诊断分析实验中最常用的一种分析方法,也常用于一些预测因素的预后准确性分析。ROC曲线对诊断的准确性提供了直观的视觉印象,曲线上的每一点代表了特定诊断方法随临界值(Cut-off值)变化时的敏感性与特异性,而曲线下面积反映诊断方法的准确情况:曲线下面积越大,诊断准确性越高。在ROC曲线上,最靠近坐标图左上方的点为敏感性和特异性均较高的临界值,一般是用于诊断的最佳临界值。ROC曲线下的面积值(Area under curve, AUC)一般在1.0和0.5之间,在AUC>0.5的情况下,AUC越接近于1,说明诊断准确性越高。一般认为AUC在 0.5~0.7时有较低准确性,AUC在0.7~0.9时有一定准确性,AUC在0.9以上时有较高准确性。 需要注意的是,很多统计软件在计算AUC时还会给出一个P值,它反映待测诊断方法的AUC和AUC=0.5之间是否有统计学差异。(实例3.7)
实例3.7 研究者开展一项前瞻性研究,分析某种lncRNA对肝癌的诊断准确性。研究者需要收集患者血液中这种特定lncRNA的水平,同时通过传统经典方法诊断肝癌作为金标准。通过将lncRNA水平和患者是否肝癌进行ROC分析,就可以得到这一种lncRNA 的AUC,同时也可以计算得出用于诊断分析的lncRNA 的临界值。 同样,如果想分析某种lncRNA对肝癌预后的影响,整个分析过程与前面差不多,只是结局换成死亡或是存活。同样可以根据是否存活进行ROC分析,得到AUC,确定这种lncRNA对预后是否有预测价值。 |
4. 生存分析
很多临床研究的最终结局指标都是生存和死亡,这一结局指标和时间密切相关,也受随访等其他因素的影响。如果想研究不同干预方法对疾病结局的影响,一般使用生存分析(Survival analysis)。生存分析是将事情发生的结局和发生这种结局所经历的时间综合起来进行分析的一种方法,它可以充分利用所收集到的数据,更加准确的评价和比较随访资料,因而能够更为全面地反映某种治疗或干预措施的效果。
生存分析中最基本的一点是计算生存时间,有完全数据(Complete data)和截尾数据(Censored data)两种,完全数据是随访期间观察到明确的结局事件(死于所研究疾病),生存时间确切,截尾数据是随访期间没有观察到明确的结局事件,截尾的原因可能是失访、死于其它疾病或随访结束时病人尚存活等,生存时间不明确。生存分析主要包括描述生存过程、生存过程比较和生存时间影响预测因素分析。
描述生存过程一般是计算出各时间点的生存率,绘制生存曲线(随访时间作为横坐标,生存率作为纵坐标),一般使用乘积极限法(Kaplan-Meier法)或寿命表法(Life table method),前者适用于样本量较小、终点或截点被准确记录的数据,主要用于未分组生存资料,后者适用于样本量较大、生存时间分段记录的数据。(实例3.8)
生存过程比较(单因素生存分析)一般用Log-rank检验,用于分析两条或多条生存曲线是否有统计学差异,其应用条件是各条生存曲线不能交叉,如果出现交叉,提示可能存在混杂因素,需使用分层分析或是多因素分析方法来校正混杂因素。
生存时间影响预测因素分析一般用Cox比例风险回归模型(Cox’s proportional hazards regression model,简称Cox回归模型),其应用条件是分析因素对生存时间的作用不随时间变化(比例风险假定),如果某种治疗手术随着观察年限延长治疗效果越差,这样的手术因素就不能纳入模型分析。
实例3.8 某科研工作者收集20例神经胶质瘤患者比较AB两种疗法的疗效,治疗的生存时间(周)如下: A组123471012232830B组351015202536374042两组的生存曲线就可以用Kaplan-Meier法绘制。 |
5. 样本量计算
临床试验在试验设计阶段就需要确定研究所需的病例数,即样本量(Sample size)。理论上,验证某一干预措施与对照之间的差异,样本量越大,试验结果越接近于真实值,即结果越可靠。但由于资源的限制和伦理原因,临床试验的样本量不可能做到无限大,因此需要确定统计学显著性检验要求的最适样本量。样本量计算时需要考虑四个参数:检验水准α、检验效能(1-β)、容许误差σ和检验的差值δ。其中α一般定义为0.05,也可定为0.01,β一般取0.2、0.1或0.05,σ和δ可以根据预实验或文献报道来设定,但是δ的设定需要有临床实际意义,比如验证一种新的降压药是否有效,如果设定δ为1 mmHg就没有什么临床实际意义,不可取。这四个参数设置越小,所需样本量越大。确定好这四个参数后,就可以使用相关软件如PASS或在线工具如http://powerandsamplesize.com/Calculators/按照相应的试验设计类型计算样本量。(实例3.9)
实例3.9 某研究者设计一个等效性临床随机对照研究,欲比较A药(一种已知价廉且安全的新药)和B药(传统药)改善贫血的疗效。据以往经验和预试验,A药可增加红细胞1.2′1012/L,B药可增加红细胞2.2′1012/L,s=1.8′1012/L,如何确定样本量? 假设两组病人数相同,我们取a=0.05,b=0.20,s=1.8′1012/L,δ=2.2′1012/L-1.2′1012/L=1.0′1012/L,通过相应的软件或是在线工具计算,如果不考虑脱落(Drop-out)或失访(Loss to follow-up),所需样本量是每组51人总计102人。 |
我们用表格总结了常用的统计分析方法及注意事项(表3.1)和不同数据所对应的常用统计分析方法(表3.2)。
表3.1 常用统计分析方法总结
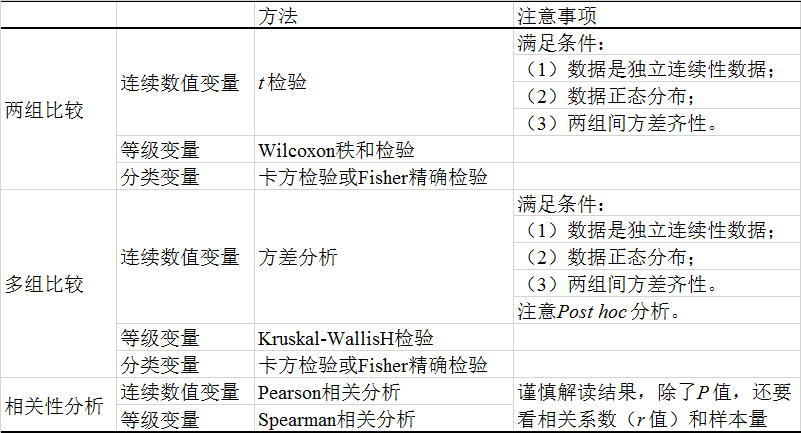
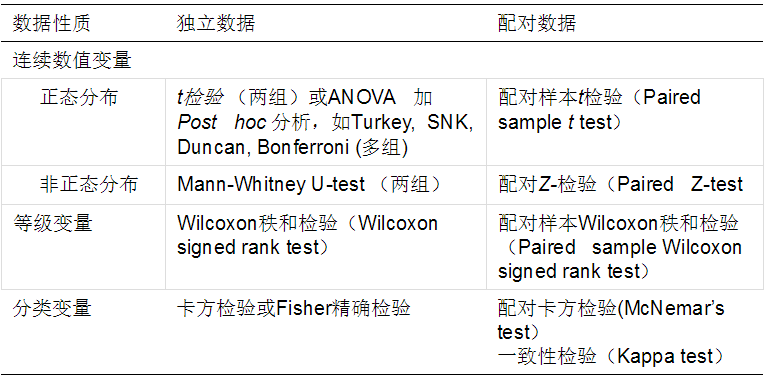
表3.2 不同数据对应的常用统计分析方法

https://m.sciencenet.cn/blog-475824-1304241.html
上一篇:基础研究常用统计方法
下一篇:科研经费的管理与使用(上)