偏微分方程PDE通常用于描述各种各样的现象，例如声、热、电、电动力学、弹性力学、流体力学等。
计算环境：Maple 2015 - Maple 2021
计算文件下载：
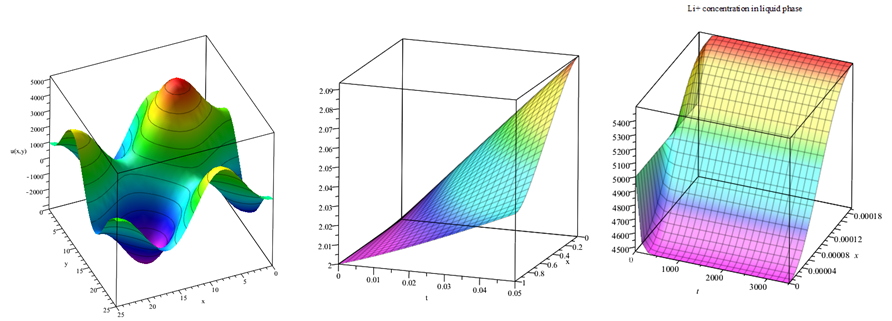
Finite difference method
approximate differential equations using finite difference equations to approximate derivatives
Collocation method
uses a finite-dimensional space of basis functions and collocation points to approximate PDEs
Galerkin's technique
uses orthogonality of a set of basis function to turn PDEs into coupled sets of ODEs
Finite difference method
The derivatives of the PDE are approximated by linear combinations of function values at the structured grid points, using a Taylor series expansion
Collocation method
Define the basis function (usually polynomials) and approximate solution:
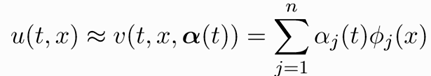
Calculate residual function by substituting the candidate function into the original PDE
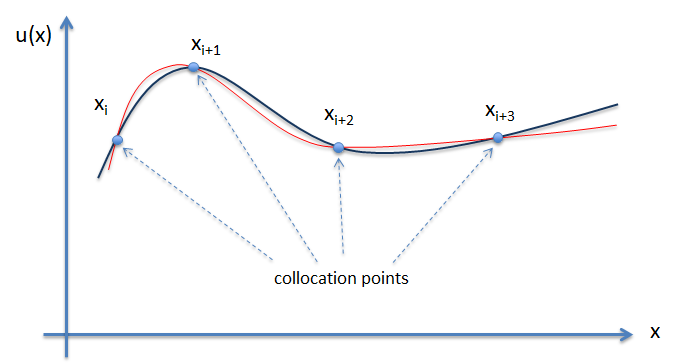
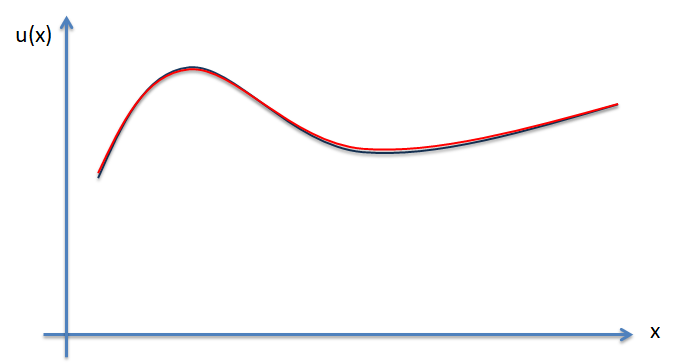
Choose the collocation points at which the candidate function must exactly match
Galerkin's method
Define the basis function (usually orthogonal polynomials) and approximate solution as
Calculate residual function by substituting the candidate function into the original PDE
Minimize the residual using Least Squares Error
Maple中的计算文件：
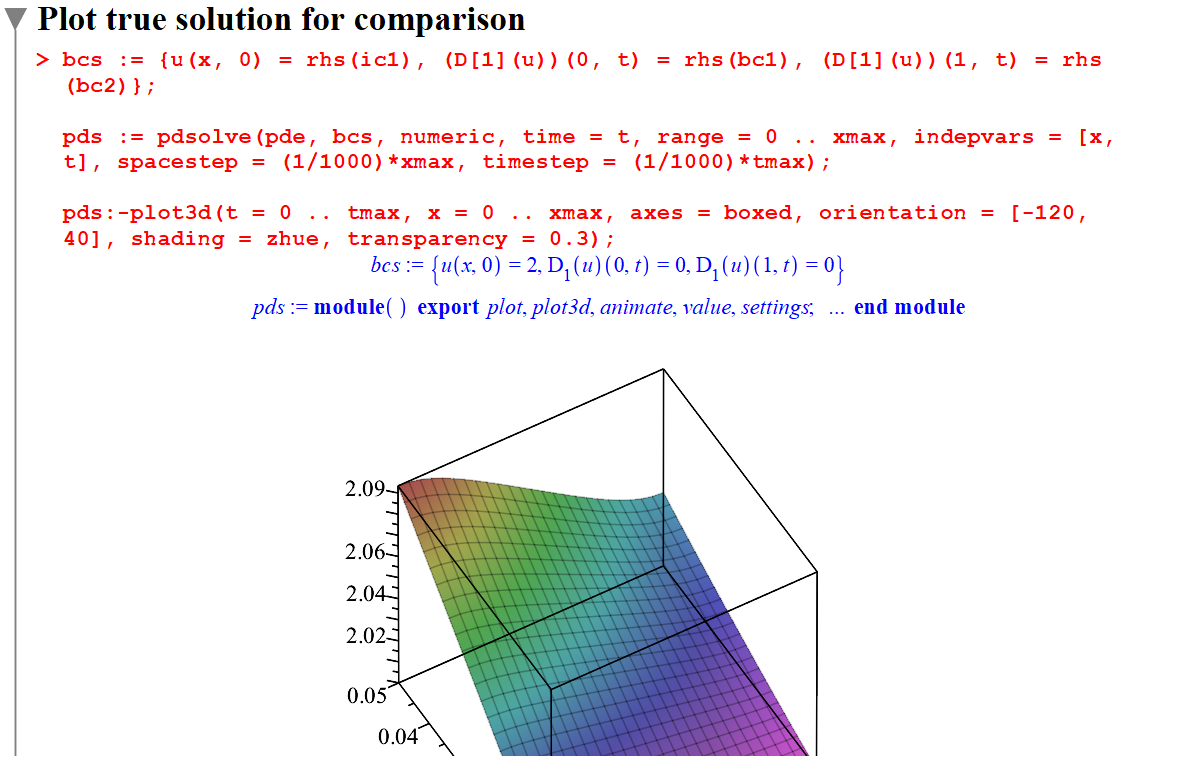
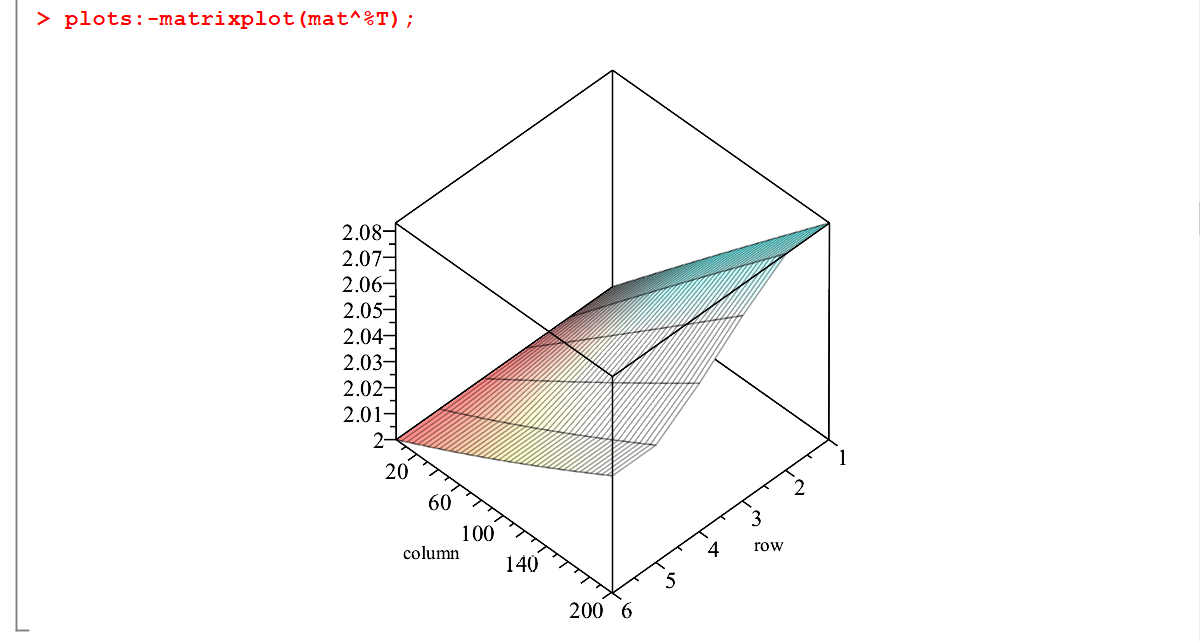
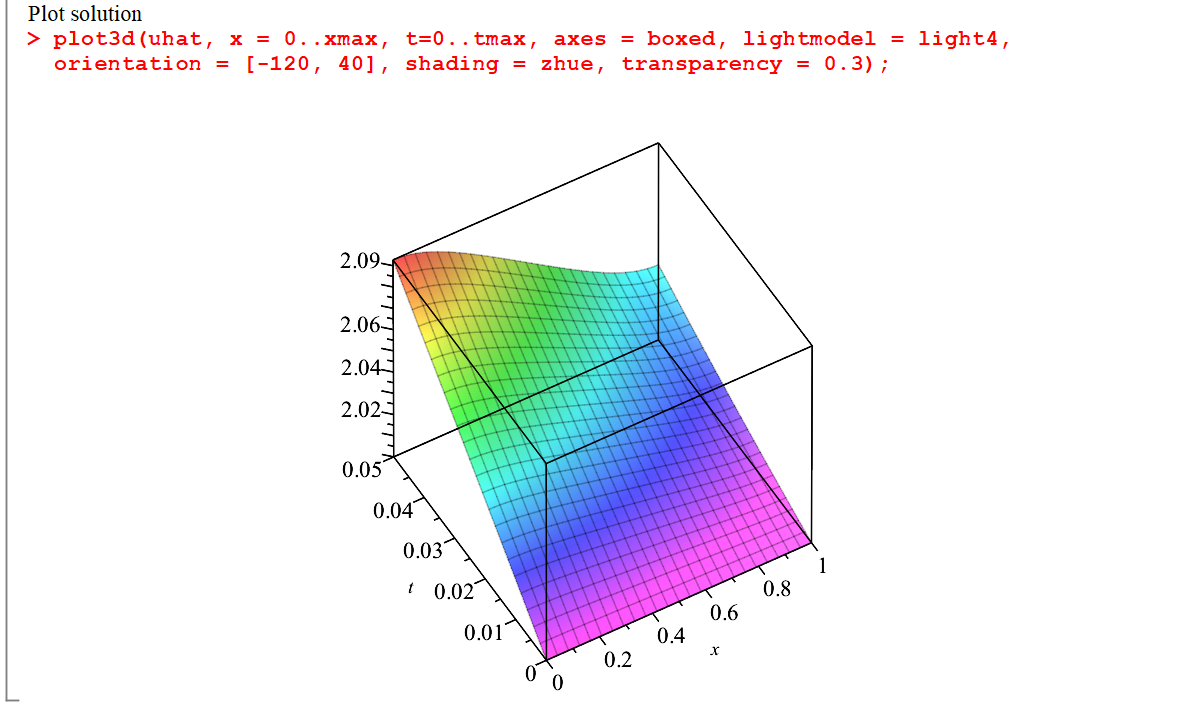
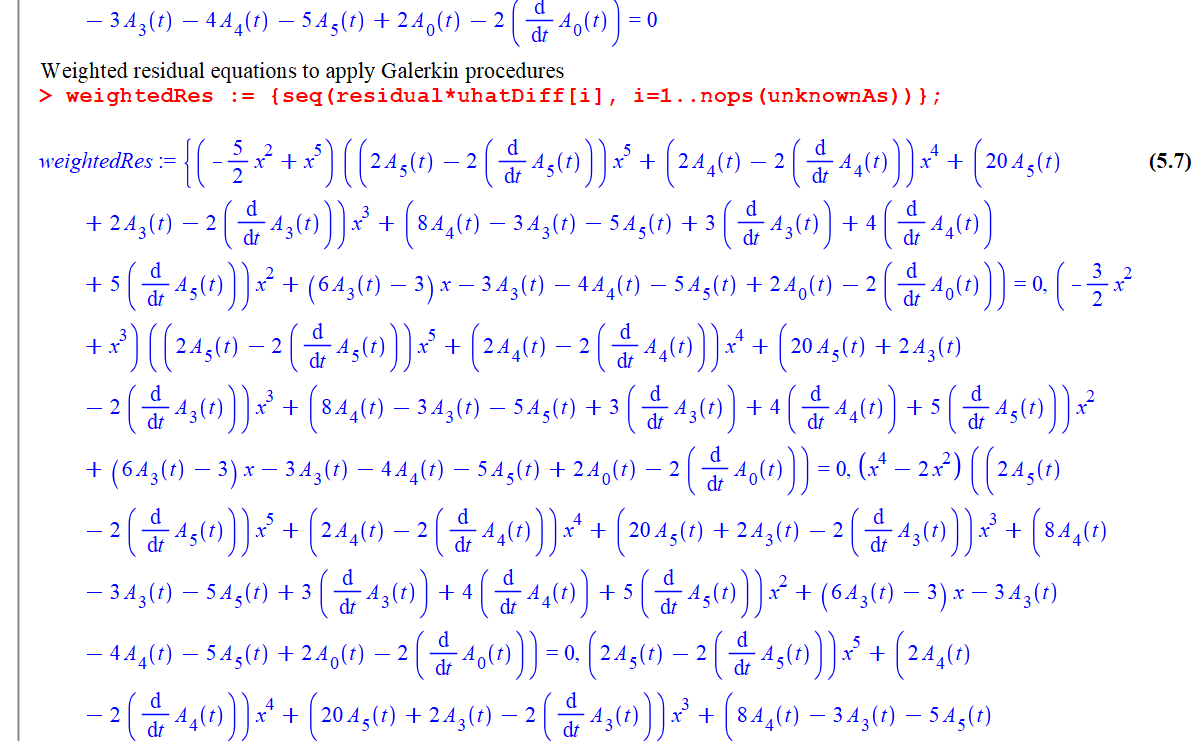
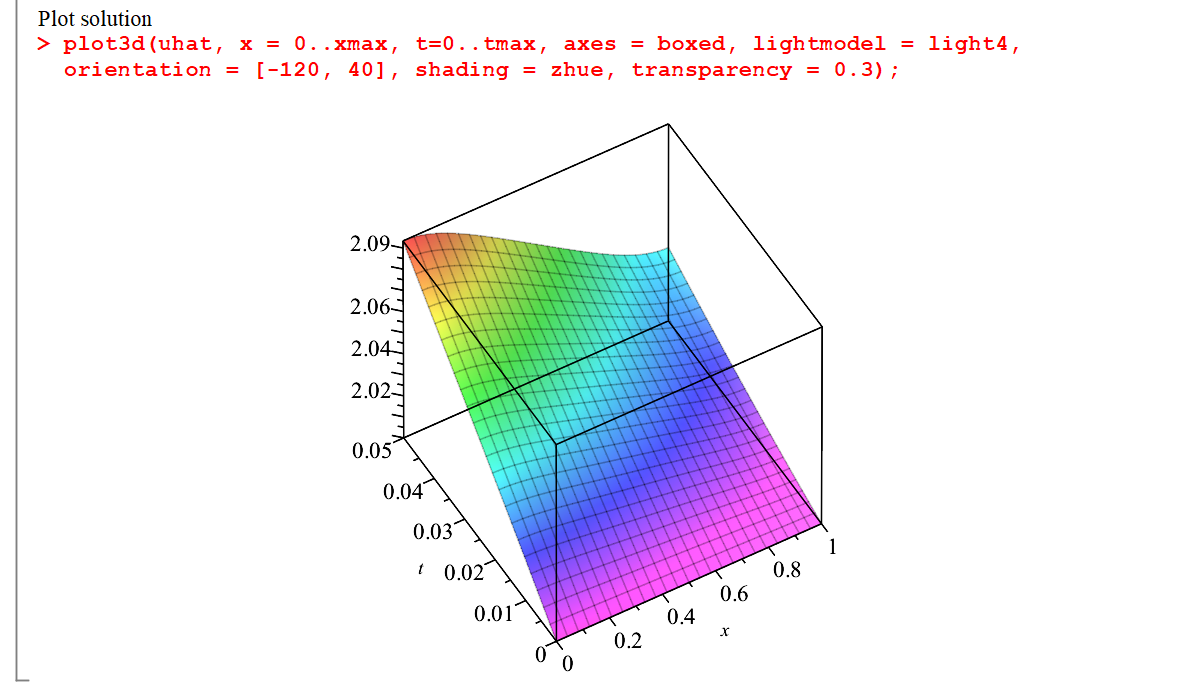
基于PDE的应用示例：
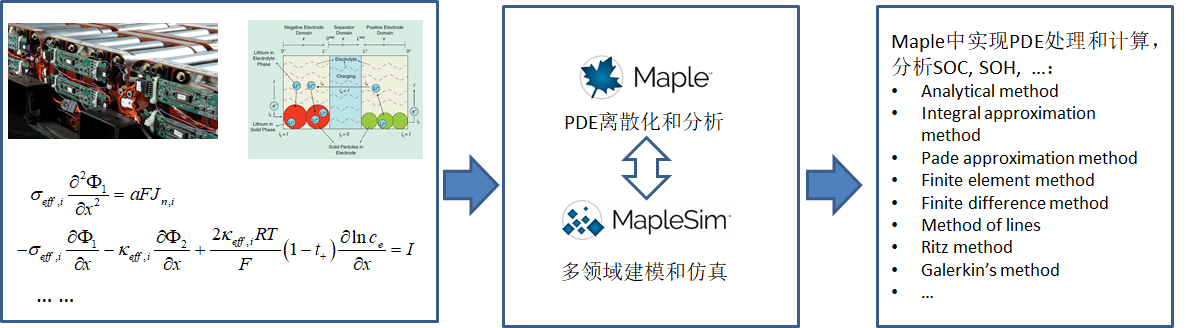
Whitepaper-Developing_Mathematical_Models_of_Batteries.pdf
转载本文请联系原作者获取授权，同时请注明本文来自徐俊林科学网博客。
链接地址：https://m.sciencenet.cn/blog-516836-1292219.html?mobile=1
收藏
