博文
《经典力学》札记: 11- 16
|
11. 为什么太阳不做圆周运动?
太阳做椭圆运动,总是让人感觉不可思议。既然做椭圆运动,那么就意味着它有一个方向距离远一点,有一个方向近一点。可是,对于各向同性的太阳,怎么会出现这个各向异性来呢?尽管这是开普勒等人的实验的结果,并得到了牛顿力学的解释,然其直观的理解,又是什么?
我们有这个疑问,是因为如果我们假设地球是被太阳牵引的,地球的速度为$v$,距离为$r$,万有引力等于离心力 $GMm/r^2 = mv^2/r$, $r = \sqrt{GM/v}$,所以地球围绕太阳运动的时间为$T = 2 \pi r^{3/2}/\sqrt{GM}$。显然,半径越大,这个周期越长。查地球到太阳距离15210万千米,水星距太阳5700万千米。地球围绕太阳一周365天,水星88天。它们的比值基本满足这个$3/2$的标度比例。所以圆周运动看起来是一个不错的描述,而且对称性上也是正确的。
这个图像的典型特点是半径$r$不变,所以$\dot{r} = 0$。但是从势的梯度---即广义力---来看,它不等于零。如果我们利用拉格朗日方程,则可以得到$m \ddot{r} = -\partial_r U(r) \ne 0$,这意味这半径不可能是固定不变的。所以,如果让它做圆周运动,是非常困难的,除非这个广义力消失。这样,这个半径一定会随着时间而改变。如果这样,半径不同,离心力不同,则速度也不同。所以我们会看到地球运动的速度也会改变。这就是椭圆推导的原因。所以从广义力的角度,它不可能为圆周轨道。通过计算发现,它是椭圆推导。牛顿力学在这里很好地解释了开普勒的实验结果。
要掌握这一部分的细节,最好借助Mathematica画图。我们考虑一个一般的势, $U \propto 1/r^a$,它会给出非常复杂的运动形式。这些形式无法通过简单的想象力获得。通过改变参数,我们还可以得到其它复杂的形式。这里我们给出$a=0.4$, 1.0, 1.1的模拟结果,只有$a=1$给出椭圆轨道,其它值给出了很漂亮的花瓣运动形式,而且不一定有闭合轨迹。这样,我们以前用离心力等于吸引力计算第一宇宙速度,只对 $1/r$ 万有引力适用,对其它力不适用。如果我们在量子力学中考虑这个问题,就不会出现这样的结构了。



12. 拉格朗日到哈密顿
很多系统,其总的能量是守恒的,所以可以借此化简微分运算。比如对于拉格朗日,可以证明$dH = 0$,其中$H = p\dot{q} - L$。这是因为\begin{equation} dH/dt = \dot{p} \dot{q} - p \ddot{q} - {\partial L \over \partial q} \dot{q} + {\partial L \over \partial \dot{q}} \ddot{q} = 0. \end{equation} 这个关系直接有$p\dot{q} - L = c$,$p = \partial L/\partial \dot{q}$。$L$可以给出动量和力的关系: $\dot{p} = \partial L/\partial q$ (牛顿方程), 以及$p = \partial L/\partial \dot{q}$(动量定义)。这个结果暗示着. $p\dot{q} = 2T$。
13. 变分法求解几个问题
1) 等周问题的最大面积。假设一个圆周长度相等,那么圆面积最大。假设这条曲线为$r(t) = (x(t), y(t))$,其长度为$I= \int_{0}^1 \sqrt{x'(t)^2 + y'(t)^2} dt = 常数$,$r(0) = r(1)$, 面积为$S = \int_0^1 (xy' - yx') dt$。我们可以计算下面的变分函数 $A = S - \lambda I$, 其中 $\lambda$为参数。利用变分原理可以得到 $2y' - \lambda {d \over dt} {x' \over \sqrt{x'^2 + y'^2}}$,类似的可以得到$x$的运动方程。做积分得到 $2(y-b) = \lambda x'/\sqrt{x'^2 + y'^2}$ ,以及$2(x-a) = -\lambda y'/\sqrt{x'^2 + y'^2}$ , 它对应圆解$(x-a)^2 + (y-b)^2 = \lambda^2$。
2)最速下降法。这个问题有很悠久的历史。假设线条满足的方程为$y=y(x)$,那么$v = \sqrt{2gy} = ds/dt$ , 其中$ds = \sqrt{1 + y'^2}dx$,所以我们有\begin{equation} \sqrt{2gy} = \sqrt{1+y'^2} dx/dt.\end{equation}我们可以定义下面的作用量最小$S = \sqrt{2g} T = \int_0^a \sqrt{1+y'^2}/\sqrt{y} dx =\int_0^a L dt$。这个方程的计算很复杂,其能量守恒得到
\begin{equation} H = py' - L = {\partial L \over \partial y'} y' - L = -{1\over \sqrt{y(1+y'^2)}} = -c. \end{equation} 所以$y(1+y'^2) = 1/c^2$。这个方程的解很复杂,我们只给出最后答案\begin{equation}y = A (1 - \cos(z)), \quad x = A (z - \sin(z)), \quad 2A = 1/c^2. \end{equation}
这两个问题各有特色,第一个问题有约束条件,第二个问题是某个函数的极小值。物理中的问题,更类似第一个问题。
14. 用Mathematica帮你求解微分方程
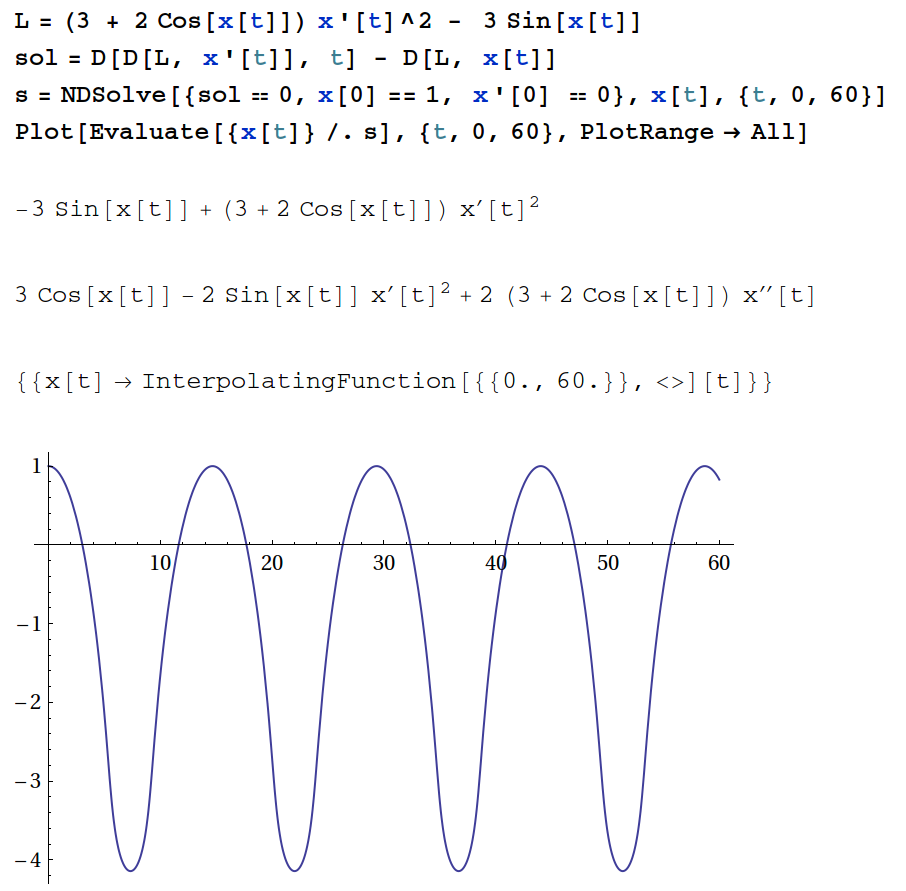
在广义坐标下,拉格朗日一般都很复杂,求解会非常麻烦,而学生又害怕做细致的推导。另外,即便是推导了,又不知道最终的结果是什么样子,怎么办?我建议学生使用Mathematica做一些推导和模拟。下面是我的一个例子。我的理论力学课程,会教学生如何做这些计算。同样地,在计算物理中,我也会讲类似的东西。
强调一点:在Mathematica中,x[t], x'[t], x''[t]等可以当作变量处理,所以计算f函数关于x'[t]的偏导,可以直接用D[f, x'[t]]计算。这会给推导带来很大的方便。Mathematica是学好物理必须具备的基本工具。
15. 关于木棍掉落的问题
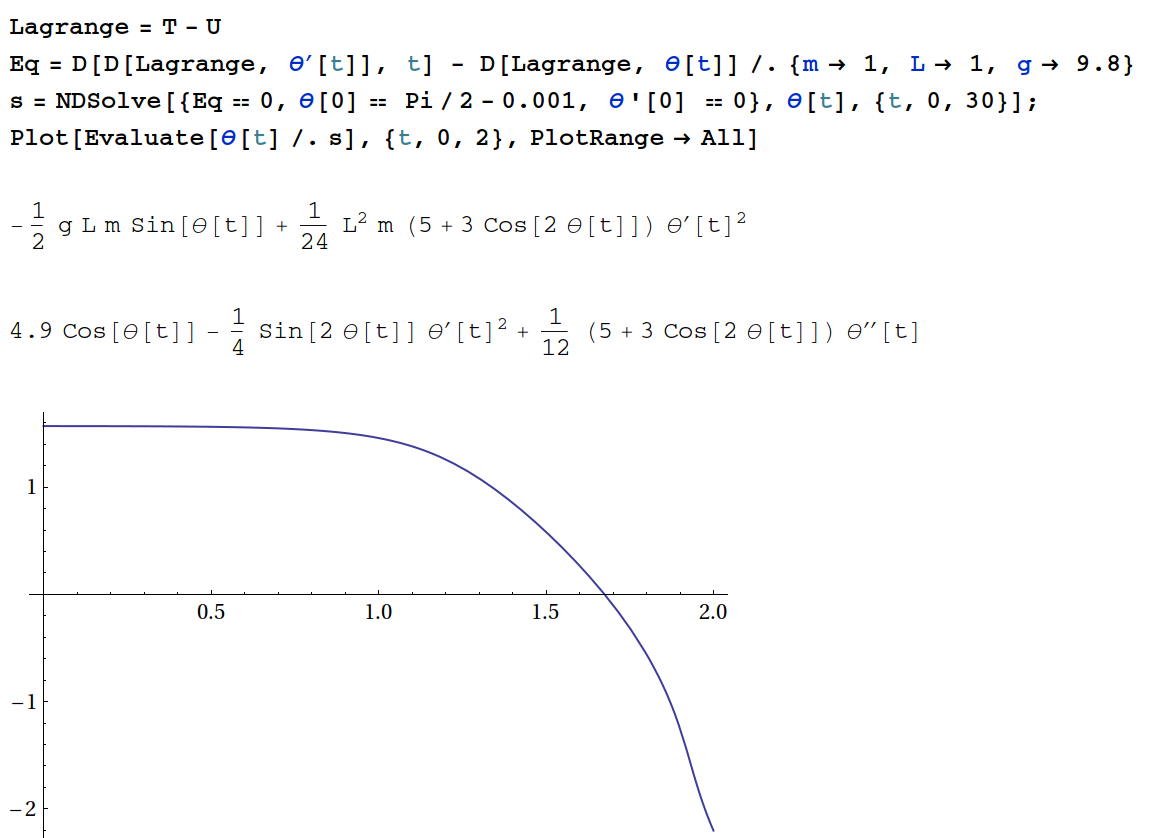
假设木棍竖立在光滑表面,问它掉落地面的时间多长? 这是一个很好的竞赛题,但是也是一个很好的经典力学题。如果这个问题改为斜面,那就更加复杂而有趣了。牛顿力学处理这样的问题不方便,但是经典力学可以。我们讨论光滑平面的情况,假设均匀木棍长度为$L$, 质量为$m$,那么在角度$\theta$的时候,它的拉格朗日为
\begin{equation} L= {m L^2\over 24} (5 + 3 \cos(2\theta(t))) \theta'(t)^2 - {g L m \over 2} \sin(\theta(t)). \end{equation} 和单摆类似,这个结果应该和质量$m$无关;从量纲上也可以分析得带这一点。我们得到的关于角度的微分方程,它是时间的函数;而时间的量纲,可以由重力加速度$g$和长度$L$得到,而和质量无关。这也是著名嗯的量纲分析的结果。这个题目,也是2021年我的《计算物理》的考试题目,当时选择这个题目的学生,约一半没有给出正确结果---可见大家对这些模拟工具不熟练。所以,这节札记,我特别强调了Mathematica的应用。

16. 用Mathematica求解微分方程并画图
我们经常需要求解各种微分方程,并画图,比如画相空间的运动轨迹。下面的代码对于处理运动方程非常有用,在教学中可以扮演重要角色。这里涉及几个命令:
1) NDSolve: 数值求解微分方程 (Numerical differential equation solver);
2)Plot画图
3)ParametricPlot, 参数画图,可以来画相空间轨迹。
Needs["PlotLegends`"]
s = NDSolve[{y'[x] == y[x] Cos[x + y[x]], y[0] == 1}, y, {x, 0, 30}];
Plot[{Evaluate[y[x] /. s], Evaluate[y'[x] /. s]}, {x, 0, 30}, PlotRange -> All, PlotLegend -> {"y[x]", "y'[x]"}, LegendPosition -> {1.1, -0.4}]
ParametricPlot[Evaluate[{y[x], y'[x]} /. s], {x, 0, 30},
PlotRange -> All, AxesLabel -> {y[x], y'[x]}]

Mathematica的确在很多情况下可以给出不错的结果,但是不要迷信这个工具,我们还是需要掌握一些别的计算工具。每个工具都有自己的优势。
https://m.sciencenet.cn/blog-709494-1353617.html
上一篇:《经典力学》札记: 1 - 10
下一篇:评布鲁克斯《几率--运气、随机和概率背后的秘密》