博文
量子与门
||
量子与门
左芬
上海微观纪元数字科技有限公司
量子计算与经典计算差别很大的地方由很多,其中之一就是,量子计算永远是可逆的,在门电路中体现为所有的门都必须是幺正的。可逆的含义就是信息不会丢失,这也就是黑洞信息疑难的由来。这一点体现得最明显的地方之一,就是经典计算中非常简单的与门,在量子计算中要大动干戈才能构建出来。
经典与门显然是丢失信息的。要保持信息的完整,首先输入输出的数目一样。将不可逆的经典门提升为可逆门的一个通用的办法是,先将输入端复制一份,用副本计算结果,再将结果存到辅助比特上去,而原始的输入比特维持不变。这样一来,二到一的与门就变成了三到三的所谓Toffoli门,可以证明确实是可逆的。将经典比特换成量子比特,Toffoli门自然地提升为量子与门。这里前两个比特因为维持不变,事实上起着控制比特的作用;而将结果存入到第三个比特上去,用的是模2加法(异或门),跟受控非门(=复制+异或,见前文)一样。所以,Toffoli门其实就是控控非门:
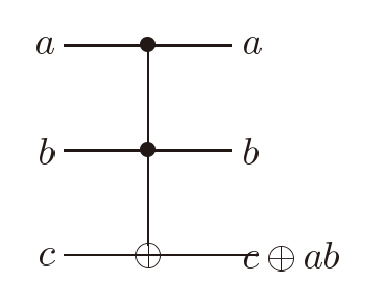
那么,怎么用基础的H,S,T以及CX门把Toffoli门具体地构建出来呢?这正是我们这里想详细讲述的内容。我们会依次介绍三种不同的电路来实现Toffoli门。
首先,把Toffoli门当成控控非门(CCX)来构建。Nielsen和Chuang的教材中介绍了多重控制门的一种递归式的构建技巧。粗略地说,就是用两个CX间隔开的Cn-1(√U)和Cn-1(√U)†来实现Cn(U)。这么说好像有点玄乎。我们来看一个简单的例子。我们知道CX是复制与异或的组合,而CZ可以通过H门作用在CX上得到。下一个不平庸的受控门是CZ的平方根,CS ,受控沿z轴旋转π/2,也叫受控相位门。根据Nielsen-Chuang的技巧,这时n=1,只需要知道C0(√S)= C0(T)=T以及T†就够了。具体做法是,先将受控比特作用T,即沿z轴旋转π/4,利用CX门将z轴掉个头,接着作用T†,最后用CX门将z轴掉转回去就行了。很容易验证,当控制比特为0时,对受控比特作用的是T T†=1; 而当控制比特为1时,对受控比特作用的是T (T†)†=T2=S,即实现了CS门。一般性的单重控制门CU的构建图如下:
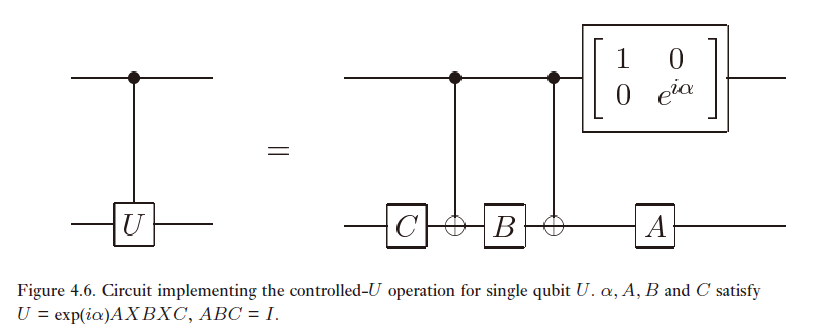
其中ABC的选择不一定是唯一的,我们刚才说的是其中一种。有了任意的CU,用类似的技巧可以递归构建任意的CCU,其构建图如下:
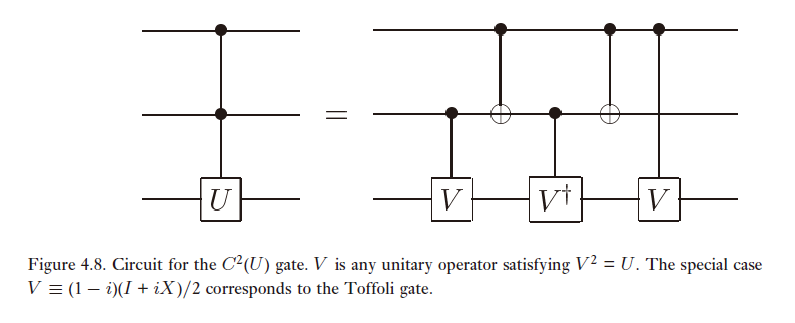
特别地,取U=X,我们得到Toffoli门:
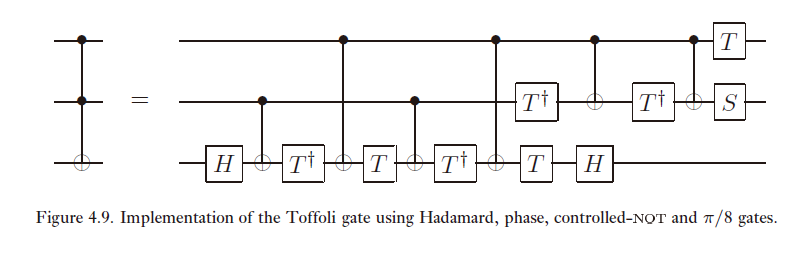
这样就得到了Toffoli门的第一种实现方式。
其次,可以利用与门的性质来构建Toffoli门。这个我是在中科院量子院(上海)的量子计算云平台与国盾量子去年底举办的首届量子计算挑战赛中学到的。具体来说,就是将与门计算用其他运算表达出来:
a∙b=-(a⊕b)/2+a/2+b/2,
这里左边表示与,右边的模2加法可以用异或门/CX实现。那么普通加减和除以2怎么实现呢?这里用的技巧是将它们放到受控旋转门的指数上去,于是a,b代表两个控制比特,正负号表示不同方向旋转,除以2表示旋转一半角度,而它们的总和变成先后旋转的总体效应。稍稍思考一下,可以得知:
Toffoli=CCX123=H3CX12CS†23CS13CS23H3,
其中123分别代表比特序号。接着再把CS/CS†门用前面提到的方法展开为基础门即可,具体的电路图我就不再画了。对比前面Nielsen-Chuang的电路图,可以发现,两者并不相同。这一点很容易看出来:CS/CS†都是用两个CX门构建的,所以这里总共用了7个CX门,而Nielsen-Chuang的图里只用到了6个。而且两者用到的T/ T†门总数也不相同。
最后,可以利用我们最近一再提到的ZX 演算来构建。ZX演算里也形成了一套递归式构建多重控制门的方法,而且比Nielsen-Chuang的方法更加直白,不需要任何技巧。不过这套方法解释起来不是那么简单,留到以后再说。我们先把Toffoli门的结果附上:
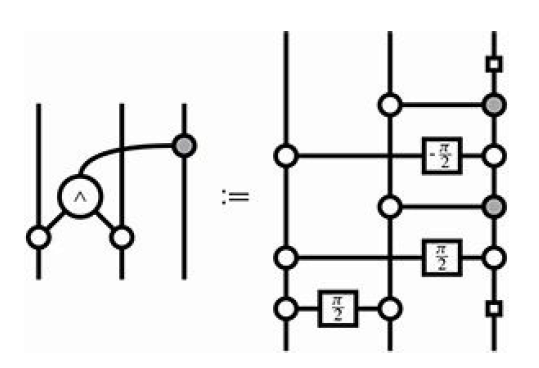
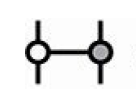
左边是Toffoli门的定义,⋀表示与。当然这是蜘蛛图,时序是从下到上的。我们可以把右图中的元素大致翻译一下。上次我们说了,CX门的蜘蛛图是:
最右边上下的方框是H门

剩下的都是这类图
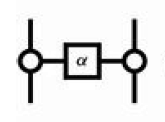
表示的是受控沿z轴旋转α角度。所以,当α=π/2时,对应的是CS门,而当α=-π/2时,对应的是CS†门。仔细数一下,你会发现这里用到了2个CX门和3个CS/CS†门,也就是总共8个CX门,所以,它与前两种构建方式又不相同。进一步,我们可以分别从CX门数目,T/T†门数目,以及非近邻控制门(所需SWAP门)数目的角度去仔细考察三种构建方式的优劣。
最后我想提一个好玩的问题。如果你并不知道这三个电路的功能,面对着三个明显不同的电路,如何判定它们是否是等价的呢?又如何将其化为最简呢?据我所知,ZX演算在这方面已经发挥了初步的作用。
https://m.sciencenet.cn/blog-863936-1338812.html
上一篇:Bob Coecke其人
下一篇:量子计算逸闻趣事
全部作者的精选博文
全部作者的其他最新博文
- • 随机性的统一理论
- • 布朗地图
- • 迷宫证明为统计力学塑造“脊梁”
- • Ising模型是NP-完全的
- • Ising模型众家谈
- • 退量子化