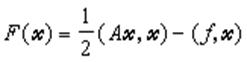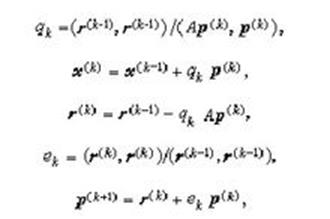博文
数值优化软件libopt v1
||||
在做优化的过程中,经常用到一些矩阵操作以及优化算法的程序,整理成了一个可用的优化工具软件libopt v1,总结在这里。
首先给出软件的下载链接:
http://pan.baidu.com/s/1jG51tmI
或者直接下载
libopt可以完成所有的矩阵操作,包括加法,减法,数乘,转置,共轭,共轭转置,行列式,特征值,特征向量,三角分解,奇异值分解等;目前libopt中实现了两种求解数值问题的常用优化方法,一种是共轭梯度法,一种是L-BFGS。所有这些操作或者优化方法都封装于类中。下面用一些demo分别介绍这些功能。其中涉及到的算法截图,如果没有特殊说明,主要来自于两本书:Nocedal and Wright, "Numerical Optimization", 2nd Ed和Golub andVan Loan 3rd ed,在后文用到的地方,不再引用赘述。
1. 矩阵的一些常用操作,包括范数、幂函数、Tanh函数、Sigmoid函数
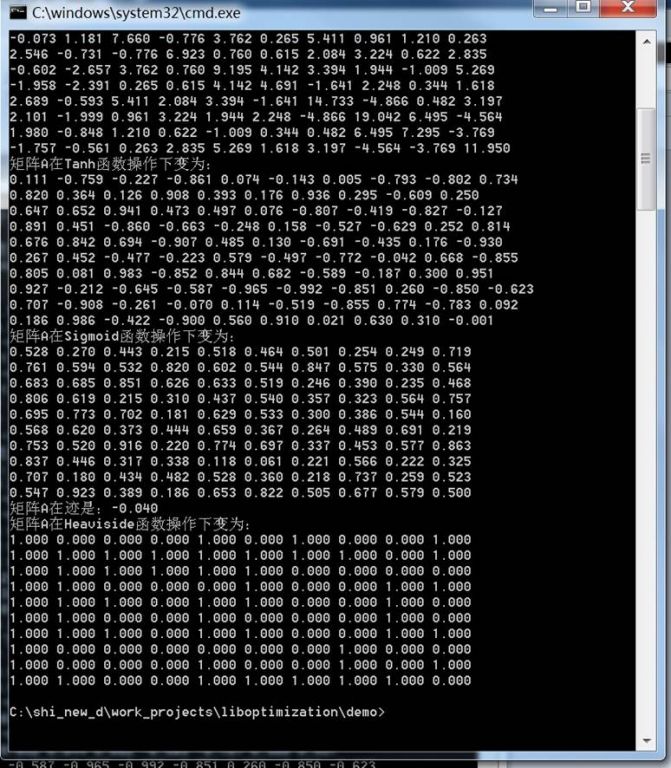
本demo显示矩阵的一些常用操作,包括范数、幂函数、Tanh函数、Sigmoid函数、求迹(Trace)、Heaviside函数等。
demo的执行方法是在包含libopt.exe的当前目录下,cmd或者dos界面下直接输入“libopt.exe0“即可。所有demo的执行中涉及到随机矩阵和随机向量的生成,因此demo执行中需要用户输入一个随机的正整数作为种子值(用于随机数生成)。
下面是执行结果:

2. 共轭梯度算法求解优化问题Ax = b
本demo显示用共轭梯度算法求解优化问题Ax = b。demo的执行方法是在包含libopt.exe的当前目录下,cmd或者dos界面下直接输入“libopt.exe 1“即可。执行的过程中我们随机生成随机正定对称矩阵A,随机向量x。
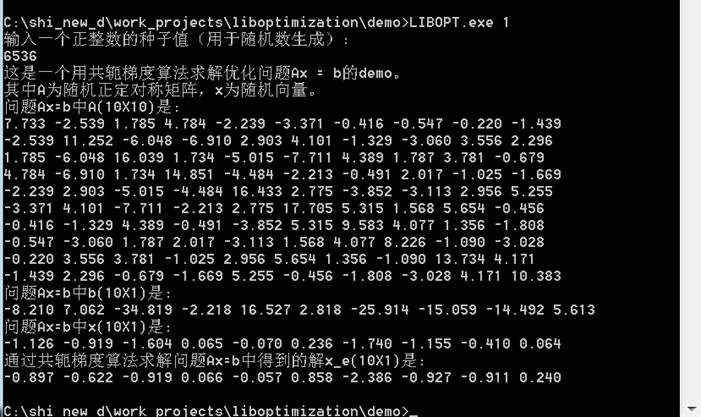
共轭梯度法(Conjugate Gradient)是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
共轭梯度法最早是由提出来在这个基础上,Fletcher和Reeves (1964)首先提出了解非线性最优化问题的共轭梯度法。由于共轭梯度法不需要矩阵存储,且有较快的收敛速度和二次终止性等优点,现在共轭梯度法已经广泛地应用于实际问题中。
共轭梯度法是一个典型的共轭方向法,它的每一个搜索方向是互相共轭的,而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合,因此,存储量少,计算方便
例如对线性代数方程组 Ax=ƒ, 式中A为n阶矩阵,x和ƒ为n维列向量,当A对称正定时,可以证明求(1)的解X*和求二次泛函
的极小值问题是等价的。由此,给定了初始向量x(0),按某一方向去求(2)式取极小值的点x(1),就得到下一个迭代值x(2),再由x(2)出发,求x(3)等等,这样来逼近x*。若取求极小值的方向为F在 x(k=1,2,…)处的负梯度方向就是所谓最速下降法,然而理论和实际计算表明这个方法的收敛速度较慢,共轭梯度法则是在 x(k-1)处的梯度方向r(k-1)和这一步的修正方向p(k-1)所构成的二维平面内,寻找使F减小最快的方向作为下一步的修正方向p(k),即求极小值的方向p(其第一步仍取负梯度方向)。计算公式为
再逐次计算
(k=1,2,…)。可以证明当i≠j时,
从而平p(1),p(2)形成一共轭向量组;r(0),r(1),…形成一正交向量组。后者说明若没有舍入误差的话,至多 n次迭代就可得到(1)的精确解。然而在实际计算中,一般都有舍入误差,所以r(0),r(1),…并不真正互相正交,而尣(0)尣(1),…等也只是逐步逼近(1)的真解,故一般将共轭梯度法作为迭代法来使用。
3. Limited-memory BFGS算法求解优化问题
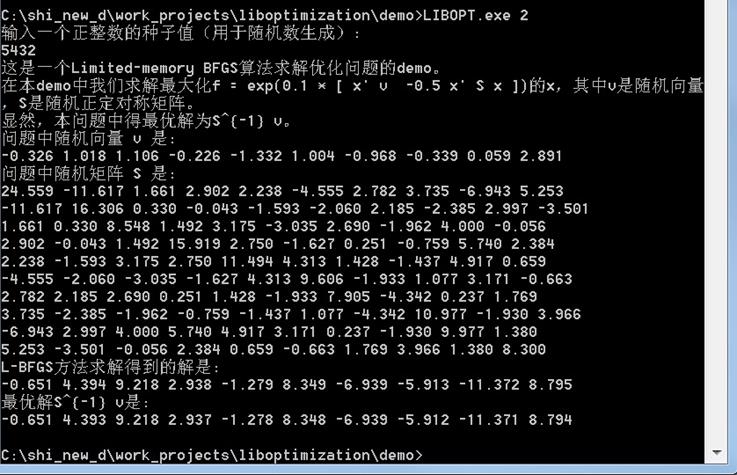
本demo显示用Limited-memoryBFGS算法求解优化问题。demo的执行方法是在包含libopt.exe的当前目录下,cmd或者dos界面下直接输入“libopt.exe 2“即可。在本demo中我们求解最大化f = exp(0.1 * [ x' v -0.5 x'S x ])的x,其中v是随机向量,S是随机正定对称矩阵。显然,本问题中得最优解为S^{-1} v。
拟牛顿法和最速下降法(SteepestDescent Methods)一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化,构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法,尤其对于困难的问题。另外,因为拟牛顿法不需要二阶导数的信息,所以有时比牛顿法(Newton'sMethod)更为有效。
拟牛顿法的基本思想如下。首先构造目标函数在当前迭代 ![]() 的二次模型:
的二次模型:
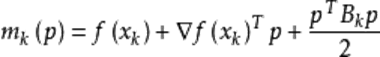
![]() 这里
这里![]() 是一个对称正定矩阵,于是我们取这个二次模型的最优解作为搜索方向,并且得到新的迭代点
是一个对称正定矩阵,于是我们取这个二次模型的最优解作为搜索方向,并且得到新的迭代点 ![]() ,其中我们要求步长
,其中我们要求步长![]() 满足Wolfe条件。这样的迭代与牛顿法类似,区别就在于用近似的Hesse矩阵
满足Wolfe条件。这样的迭代与牛顿法类似,区别就在于用近似的Hesse矩阵 ![]() 代替真实的Hesse矩阵。所以拟牛顿法最关键的地方就是每一步迭代中矩阵
代替真实的Hesse矩阵。所以拟牛顿法最关键的地方就是每一步迭代中矩阵 ![]() 的更新。现在假设得到一个新的迭代
的更新。现在假设得到一个新的迭代 ![]() ,并得到一个新的二次模型:
,并得到一个新的二次模型:
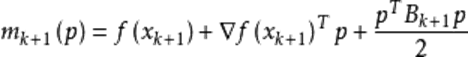
我们尽可能地利用上一步的信息来选取 ![]() 。具体地,我们要求
。具体地,我们要求 ![]() ,从而得到
,从而得到
![]()
BFGS公式为

由他产生的矩阵 ![]() 同样保持正定性,而且也满足一个极小性:
同样保持正定性,而且也满足一个极小性:
![]()
Nodecdal& Wright 在他们的书 "Numerical Optimization"
![]()

L-BFGS即Limited-memory BFGS,在之前的BFGS算法中,我们可以不存储矩阵![]() ,而是存储最近
,而是存储最近![]() 次迭代的曲率信息,即
次迭代的曲率信息,即![]() 和
和![]() 。当完成一次迭代后,最旧的一次曲率的信息将被删除,而最新的曲率将被保存下来,所以这样就保证了保存的曲率信息始终都来自最近的
。当完成一次迭代后,最旧的一次曲率的信息将被删除,而最新的曲率将被保存下来,所以这样就保证了保存的曲率信息始终都来自最近的![]() 次迭代。在实际工程中
次迭代。在实际工程中![]() 取3到20之间的值效果比较好。
取3到20之间的值效果比较好。
将上面的公式整理一下,一直递推![]() 次下去,就有
次下去,就有
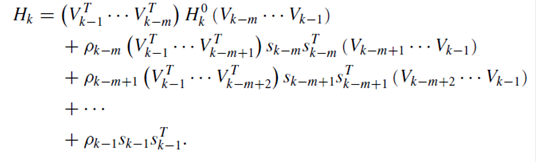
以上的公式用算法形式描述如下:

此时L-BFGS可以用算法描述如下:

L-BFGS方法的局限性:Themain weakness of the L-BFGS method is that it converges slowly onill-conditioned problems—specifically, on problems where the Hessian matrix contains a widedistribution of eigenvalues.
Wolfe准则
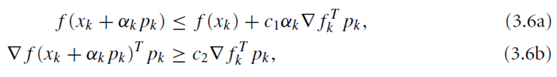
![]()
例子DEMO:
最小化f =exp(0.1 * [ x' v -0.5 x' S x ]),最优解是S^{-1} v。L-BFGS是一个迭代的过程,从上面的算法中可以看出,每一次迭代需要计算两个量:一个是hessian矩阵的计算,也就是搜索方向的确定(ComputeNewDirection),另一个是步长的计算(StepSizeIteration);退出条件一般设为最近若干次迭代中使用的步长足够小。Hessian矩阵的初始化,一般是通过
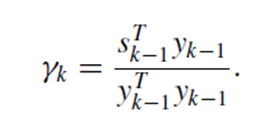
来进行的。
实验显示精度很高。
4. 矩阵求逆
这是一个矩阵求逆demo,输入定矩阵A是我们生成的高斯随机10X10矩阵。输出为该矩阵的逆矩阵。demo的执行方法是在包含libopt.exe的当前目录下,cmd或者dos界面下直接输入“libopt.exe 3“即可。
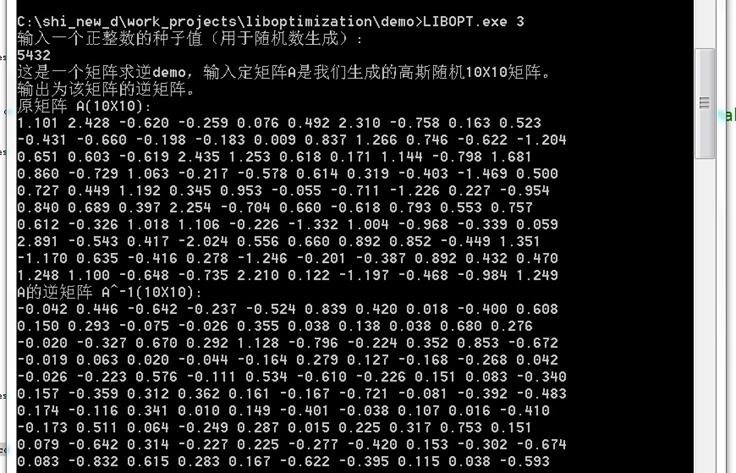
5. 矩阵三对角化
这是一个矩阵三对角化demo,通过对对称正定矩阵A做变换T = Q AQ^T,得到三对角化矩阵T,其中Q是正交矩阵。在本demo中,输入正定矩阵A是我们生成的高斯随机10X10矩阵。demo的执行方法是在包含libopt.exe的当前目录下,cmd或者dos界面下直接输入“libopt.exe 4“即可。

通过对对称正定矩阵A做变换T = Q AQ^T,得到三对角化矩阵T,其中Q是正交矩阵。当然在这种变化之后,矩阵的迹是不会变的。以下是变化算法。



6. QR算法求解矩阵特征值
这是一个QR算法求解矩阵特征值的demo,将矩阵A首先三对角化B= P AP^T得到矩阵B。然后对B做QR分解,得到乘积B= QR,其中Q为正交矩阵,而R为对角矩阵。在本demo中,输入矩阵A是我们生成的高斯随机10X10正定对称矩阵。而A和R的关系为R= Q^TP A P^T。
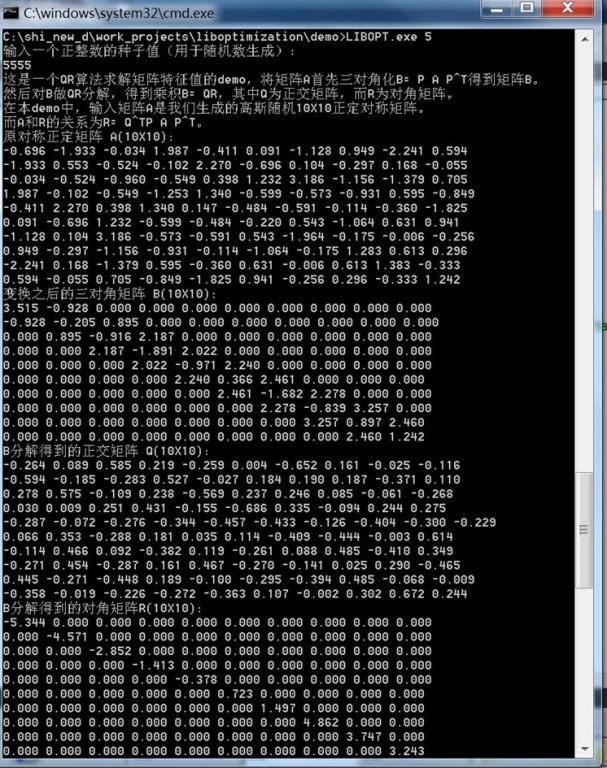
QR分解(QRdecomposition)是指将矩阵A分解成两个矩阵的乘积A = QR,其中Q为正交矩阵,而R为上三角矩阵。QR分解可以用来求解线性最小二乘问题,同时也是求解特征值算法QR算法(the QR algorithm)的基础。

7. 矩阵特征值
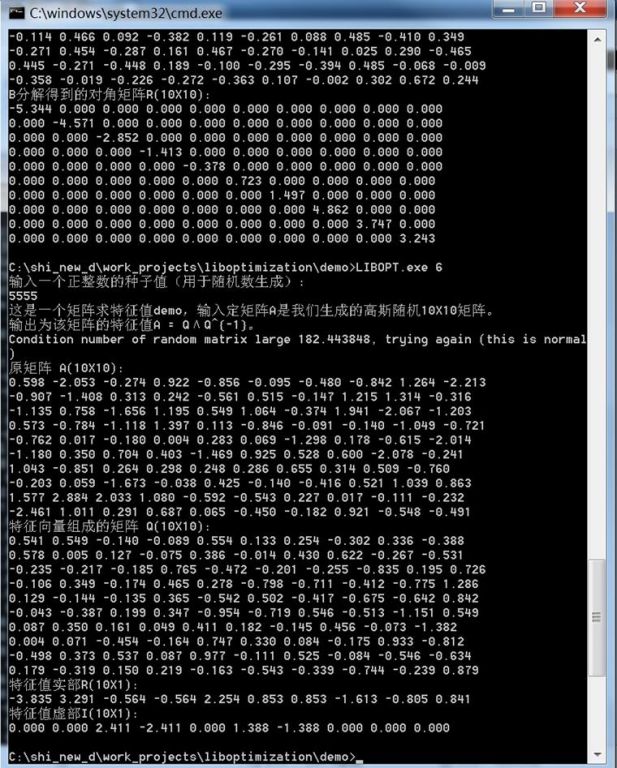
这是一个矩阵求特征值demo,输入定矩阵A是我们生成的高斯随机10X10矩阵。输出为该矩阵的特征值A= QΛQ^{-1}。
满足![]() 的非零向量叫做矩阵A的特征向量,而对应的λ称为特征值。假设
的非零向量叫做矩阵A的特征向量,而对应的λ称为特征值。假设![]() 是所有的特征向量,则矩阵A可以分解成
是所有的特征向量,则矩阵A可以分解成![]() ,其中Λ为对角矩阵,其中的元素则为所有的特征值。
,其中Λ为对角矩阵,其中的元素则为所有的特征值。

https://m.sciencenet.cn/blog-907554-934404.html
上一篇:波尔图 塞拉阿尔维斯(Serralves)当代艺术博物馆游记
下一篇:婴儿哭声监测软件 LilyBabyCryingDetector v1.0