博文
广义线性模型中的逻辑斯蒂回归
|||
其实题目不太准确,这篇短文介绍的是二项分布线性模型, 也就是当响应变量为01时的线性模型,例如物种是否出现,病人是否需要住院,学生是否成功考入大学,英语四六级成绩是否及格等。逻辑斯蒂回归模型,是二项分布线性模型中的一种,也是最广泛的一种。
事情还要从1935年说起。那一年,英国伦敦大学学院的C.I. Bliss 在《Annals of Applied Biology》上发表论文The Calculation of the Dosage-Mortality Curve。这篇论文的表4,就是现在广泛用于逻辑斯蒂回归教学的beetle数据。该数据是C.I. Bliss从Strand在1930年发表的论文中摘出来的。
Bliss的这篇论文主要以杂拟谷盗(Tribolium confusum)为例,系统介绍拟合存活比例曲线的方法。杂拟谷盗是一种粮食害虫。当时生物学家将481只杂拟谷盗分成8组,每一组分别在暴露在不同浓度的二硫化碳5小时,之后记录每个组有多少只甲虫死了。由于甲虫对二硫化碳的反应只有两种可能,要么存活,要么死亡,所以这个数据集是典型的二项分布数据。
在这篇论文中,Bliss提出了一种连接函数,也就是事件发生与否,用转换以后的正态分布累计曲线去估算,称为Probit。实际上,二项分布线性模型的连接函数有三种,分别为logit, probit以及cloglog。 logit、probit以及cloglog都是统计变换,目的是将二项分布数据转换为一种形式,以便能用线性模型估计直接估计模型的参数。其中最常见的为logit,使用logit连接函数的二项分布回归称为逻辑斯蒂回归。logit是事件发生与是否发生的比例 (odds)的对数值,形为log(y/(1-y)),称为log odds。cloglog是complementary log log的缩写,是将响应变量进行两次log变换, 公式为log(-log(1-y))。 cloglog常用来拟合数据出现大量极端数值的数据, 例如,大样地的幼苗的负密度制约研究中,部分胸径等级的树苗只有很少一部分死亡,用cloglog能较准确捕捉到与树苗死亡相关性较强的环境因子, 如同种密度制约、光环境等。
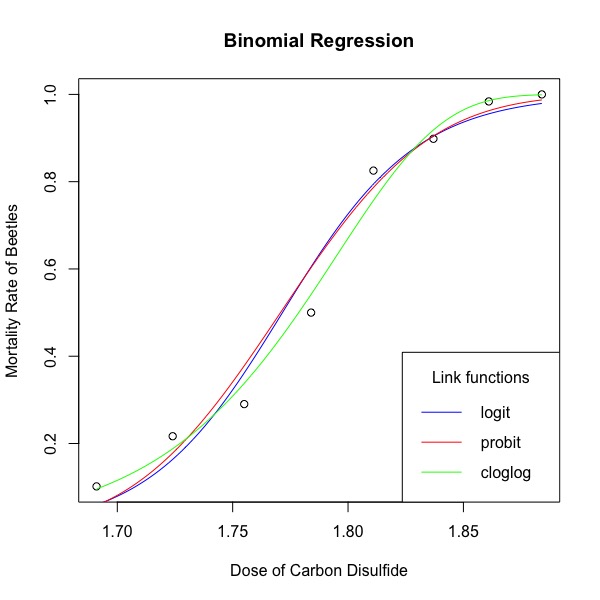
下面用R代码演示如何进行二项分布回归,分别用logit, probit以及cloglog三种连接函数。
library(broom)
####表格形式的数据
####tabular form
####数据来源www.stat.ualberta.ca/~kcarrier/STAT562/comp_log_log
####beetle
#### LOGDOSE NUMBER_OF_BEETLES NUMBER_KILLED COMP_LOG_LOGPROBITLOGIT
####1 1.691 59 6 5.7 3.4 35.0
####2 1.724 60 13 11.3 10.7 9.8
####3 1.755 62 18 20.9 23.422.4
####4 1.784 56 28 30.3 33.8 33.9
####5 1.811 63 52 47.7 49.6 50.0
####6 1.837 59 53 54.2 53.4 53.3
####7 1.861 62 61 61.1 59.7 59.2
####8 1.884 60 60 59.9 59.2 58.8
####>
####二硫化碳的浓度
LOGDOSE <-c(1.691, 1.724, 1.755, 1.784, 1.811, 1.837, 1.861, 1.884 )
####各小组杂拟谷盗的头数
NUMBER_OF_BEETLES<-c(59, 60, 62, 56, 63, 59, 62, 60 )
####杂拟谷盗经过二硫化碳熏蒸5小时后,死亡的个体数
NUMBER_KILLED <-c(6, 13, 18, 28, 52, 53, 61, 60 )
####合并成一个数据框
beetle<-data.frame(NUMBER_OF_BEETLES,NUMBER_KILLED, LOGDOSE)
####第一种方法,数据表格式
####调用glm函数,注意连接函数的选择
mod_logit <-glm(cbind(NUMBER_KILLED, NUMBER_OF_BEETLES -NUMBER_KILLED)~LOGDOSE,data=beetle, family=binomial(link="logit") )
mod_probit <-glm(cbind(NUMBER_KILLED, NUMBER_OF_BEETLES -NUMBER_KILLED)~LOGDOSE,data=beetle, family=binomial(link="probit"))
mod_cloglog<-glm(cbind(NUMBER_KILLED, NUMBER_OF_BEETLES -NUMBER_KILLED)~LOGDOSE,data=beetle, family=binomial(link="cloglog"))
####Showing significance of the variables
tidy(mod_logit )
## term estimate std.error statistic p.value
##1 (Intercept) -60.74013 5.181870 -11.72166 9.871561e-32
##2 LOGDOSE 34.28593 2.913213 11.76911 5.631446e-32
tidy(mod_probit)
## term estimate std.error statistic p.value
##1 (Intercept) -34.95614 2.648984 -13.19605 9.245343e-40
##2 LOGDOSE 19.74103 1.488046 13.26640 3.625628e-40
tidy(mod_cloglog)
## term estimate std.error statistic p.value
##1 (Intercept) -39.52224 3.235649 -12.21463 2.596958e-34
##2 LOGDOSE 22.01474 1.796996 12.25085 1.662370e-34
####Showing AIC et al.
glance(mod_logit )
## null.deviance df.null logLik AIC BIC deviancedf.residual
##1 284.2024 7 -18.65681 41.31361 41.4725 11.11558 6
glance(mod_probit)
## null.deviance df.null logLik AIC BIC deviancedf.residual
##1 284.2024 7 -18.0925 40.18499 40.34388 9.986957 6
glance(mod_cloglog)
## null.deviance df.null logLik AIC BIC deviancedf.residual
##1 284.2024 7 -14.85619 33.71237 33.87126 3.514334 6
####绘图Visualisingthe results
mortality_rate<-beetle$NUMBER_KILLED/beetle$NUMBER_OF_BEETLES
dose<-beetle$LOGDOSE
plot(mortality_rate~dose,xlab="Dose of Carbon Disulfide",ylab="MortalityRate of Beetles",main="BinomialRegression")
LOGDOSE_new=seq(min(dose),max(dose),length.out=200)
mod_logit_line <-predict(mod_logit,newdata=data.frame(LOGDOSE=LOGDOSE_new), type="response")
lines(mod_logit_line~LOGDOSE_new,col="blue")
mod_probit_line <-predict(mod_probit,newdata=data.frame(LOGDOSE=LOGDOSE_new), type="response")
lines(mod_probit_line~LOGDOSE_new,col="red")
mod_cloglog_line <-predict(mod_cloglog,newdata=data.frame(LOGDOSE=LOGDOSE_new), type="response")
lines(mod_cloglog_line~LOGDOSE_new,col="green")
legend("bottomright",title="Linkfunctions",legend=c("logit","probit","cloglog"),lty=c(1,1,1),col=c("blue","red","green"))
#####第二种方法,每个个体生存状态的长数据格式。glm是可以接受这种格式的。
#####按照个体来计
dose_surived<-
c(rep(1.691,59-6),
rep(1.724,60-13),
rep(1.755,62-18),
rep(1.784,56-28),
rep(1.811,63-52),
rep(1.837,59-53),
rep(1.861,62-61),
rep(1.884,60-60))
dose_dead<-c(
rep(1.691, 6),
rep(1.724,13),
rep(1.755,18),
rep(1.784,28),
rep(1.811,52),
rep(1.837,53),
rep(1.861,61),
rep(1.884,60))
status_survived<-c(
rep("alive",59-6),
rep("alive",60-13),
rep("alive",62-18),
rep("alive",56-28),
rep("alive",63-52),
rep("alive",59-53),
rep("alive",62-61),
rep("alive",60-60))
status_dead<-c(
rep("dead", 6),
rep("dead",13),
rep("dead",18),
rep("dead",28),
rep("dead",52),
rep("dead",53),
rep("dead",61),
rep("dead",60)
)
dose_long<-c(dose_dead,dose_surived)
status <-as.factor(c(status_dead,status_survived))
incidence_mod_logit <-glm(status~dose_long,family=binomial(link="logit"))
incidence_mod_probit <-glm(status~dose_long,family=binomial(link="probit"))
incidence_mod_cloglog<-glm(status~dose_long,family=binomial(link="cloglog"))
####Showing significance of the variables
tidy(incidence_mod_logit )
## term estimate std.error statistic p.value
##1 (Intercept) -60.74013 5.181834 -11.72174 9.861985e-32
##2 dose_long 34.28593 2.913192 11.76920 5.625873e-32
tidy(incidence_mod_probit)
## term estimate std.error statistic p.value
##1 (Intercept) -34.95613 2.649010 -13.19592 9.261453e-40
##2 dose_long 19.74102 1.488061 13.26627 3.631968e-40
tidy(incidence_mod_cloglog)
## term estimate std.error statistic p.value
##1 (Intercept) -39.52224 3.235632 -12.21469 2.594819e-34
##2 dose_long 22.01474 1.796986 12.25092 1.660982e-34
####Showing AIC et al.
glance(incidence_mod_logit )
## null.deviance df.null logLik AIC BIC deviancedf.residual
##1 645.441 480 -186.1771 376.3542 384.7059 372.3542 479
glance(incidence_mod_probit)
## null.deviance df.null logLik AIC BIC deviancedf.residual
##1 645.441 480 -185.6128 375.2255 383.5773 371.2255 479
glance(incidence_mod_cloglog)
## null.deviance df.null logLik AIC BIC deviancedf.residual
##1 645.441 480 -182.3765 368.7529 377.1046 364.7529 479
https://m.sciencenet.cn/blog-255662-1081614.html
上一篇:大型森林样地样方的命名与坐标转换
下一篇:繁花满树 (十六首)