博文
心脏支架、折纸艺术与超材料设计
||
文/陈仕魁(纽约州立大学石溪分校机械工程系助理教授)
顾险峰(纽约州立大学石溪分校计算机系终身教授,清华大学丘成桐数学科学中心访问教授。)
泊松比(Poisson's ratio)是力学中的一个概念,它的定义是材料受到纵向压力(或拉力)的时候,在弹性范围内它的横向变形量与纵向变形量的比值,泊松比也叫横向变形系数。人们在日常生活中所见到的大部分材料的泊松比都在0~0.5之间,例如:空气的泊松比为0,铝的泊松比为0.33,水的泊松比为0.5。传统材料受到外力挤压的时候,在压力作用的方向会收缩,而同时在垂直于压力的方向会发生膨胀。而负泊松比材料则正好相反,当负泊松比材料受到外界压力的时候,其同时会在平行与垂直于外力的方向发生收缩。负泊松比材料在军事、航天航空、汽车、船舶、医疗、体育用品等各个行业有着广泛用途。负泊松比特性很大程度上是由其微观几何结构所决定。所以可以通过设计其微观结构来获得所需的材料特性,这也催生了一个新兴的研究领域——超材料设计(metamaterial design)。心脏支架就是一个几何、材料、机械和医学等多个学科结合的例子。
心脏支架(图1),又称冠状动脉支架,是一种常见的手术器材。从功能上分析,动脉支架具有收缩和膨胀两种状态,收缩的时候体积应该尽量的小,从而可以顺利通过动脉血管。用传统材料制成的动脉支架在圆周径向收缩时,会在圆柱的纵向拉伸,即具有正泊松比。但是在动脉支架的应用中,人们希望找到一种理想材料,当径向压缩支架时,其纵向长度也收缩,即具有负泊松比的材料。这样,手术风险会被降低。
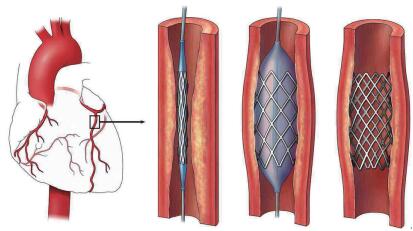
图1 动脉支架收缩前后示意图(图片来源:搜狐网)
自然界中所有的材料都具有正泊松比,负泊松比材料只能被人工制造出来。负泊松比的弹性形变特性是由材料微观结构的几何模式决定的。图2显示了具有负泊松比的动脉支架,它是最近被发明出来的新型支架。整体上,在收缩状态,材料比较致密,体积较小;而在膨胀时,材料是各项同性的,向各个方向均匀扩张。

图2 具有负泊松比的心脏支架
负泊松比材料的微观结构具有高度的对称性。历史上最早的负泊松比材料来自于折纸艺术,折纸激发出许多负泊松比材料设计的灵感。古典的折纸艺术不允许使用剪刀、浆糊,只能沿着折痕折叠,如图3所示的魔球。

图3 折出的魔球
当魔球形变时,纸上任意两点之间(在纸面上)的最短路径保持不变,任意两点间的测地距离也不改变。这种形变被称为是等距形变(isometric deformation)。当表面发生等距形变时,内部体的形状也发生改变,这种曲面被称为是柔性曲面(flexible surface)。
普通的纸张材质比较刚硬,容易折成四面体、六面体这样的刚性曲面,很难构成自由曲面。但是,一旦折叠成自由曲面之后,整体柔性增加了很多,可以用于形变成各种形状。
一个封闭曲面,如何判定它是否具有刚性,是一个古老的几何命题。这个问题的一种解决思路与广义相对论有关。在广义相对论中,爱因斯坦度量描绘了时空的几何。
给定一个多面体曲面,可以用数学的方法来判定它是刚性还是柔性的。如图4所示,左侧多面体是刚性的,右侧是柔性的。首先,需将多面体曲面的内部进行三角剖分,得到一个四面体网格(有时,需在多面体内部加入顶点才能得到三角剖分)。然后,结合Schlafli定理计算希尔伯特-爱因斯坦能量的海森矩阵(Hessian Matrix),如果零空间的维数等于内顶点个数的3倍,那么多面体具有刚性;否则,多面体具有柔性。海森矩阵零空间的维数反应了origami的柔性维度。

图4 刚性多面体(左)和柔性多面体(右)
柔性几何为超材料设计提供了理论依据。目前,人们对于柔性几何的研究才刚刚开始,无论在理论上,还是在实际中都有很多尚未解决的问题,也是非常具有潜力的方向。在这里,人们又一次看到自然真理的普遍联系:古老的折纸和广义相对论出乎意料地紧密结合。人们期待着机械力学、材料科学和现代几何的一场深刻合作。
(责任编辑 王丽娜)
https://m.sciencenet.cn/blog-336909-1060484.html
上一篇:科技发展助推中国崛起
下一篇:产学研合作要有诚信