博文
Science“驴得水”论文中的统计错误
|
2021年4月21号,Science发表了一篇论文,该研究发现,美国亚利桑那沙漠中的 “野驴挖井”现象会使起来动物渔翁得利,也能利用这些“井”中的水资源,进而有缓解生物多样性的丧失(Lundgren et al. 2021)。

这篇据说是靠“众筹”完成的“驴得水”论文一经发表,便引起了广泛报道。比如:

细看这篇论文,研究确实很有意思,其数据分析颇值得同行借鉴。该研究用了广义线性混合模型(glmm)对数据进行分析,并考虑了数据的过度离散。其统计方法中,部分描述如下:
We then used generalized linear mixed effect models in the R package ‘glmmTMB’ v1.0.1 to analyze how resource types (i.e. equid wells, background waters, and dry controls) and environmental variables influenced vertebrate activity. We chose distributions appropriate for each response variable and nested date within site as a random effect. …we used zero-inflated mixed effect models with season nested within site as a random effect…
注意红字部分,这里的glmm模型是以日期嵌套在地点(site)之下为随机效应,这也是跟其实验设计相匹配的,这么做没有问题。上述模型均采用glmmTMB包完成,其分布类型则用到了零膨胀泊松,零膨胀负二项,零膨胀gamma等。该论文附件中有数据和代码,其模型结构基本如下:
richness.cels.glmmad.poisson <- glmmTMB(richness ~ water + tmax + last_3_ppt + (water:tmax)+ (water:last_3_ppt)+(1|numeric_day/site), data=all_water.div, ziformula = ~1, family=poisson)
同样,注意红字部分,其中site即为地点,numeric_day即为日期。那么问题来了,原代码中(1|numeric_day/site)这种设置,竟然是错误的。因为glmmTMB在设置嵌套型随机效应时,上层单位,应写在前面,下层单位,应写在后面,即代码应该是(1| site/ numeric_day),这才是将日期嵌套在地点之内的正确写法(事实上lme4, nlme, brms等常用混合模型工具包都是这种格式)。想详细了解到道友,可以参考glmmTMB包的主要作者之一Ben Bolker(这位大师也是混合模型第一包lme4包的作者)的介绍文章中的相关描述,如下图所示:


事实上,如果我们查看上述错误模型的结果(如下图所示),也很容易发现问题:
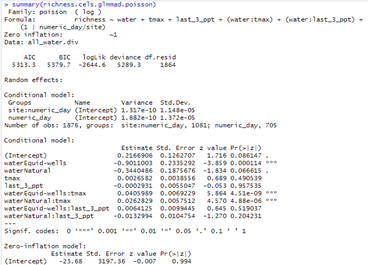
注意红框中结果,两个随机效应,造成的方差都非常小,达到了10的-10次方的级别!也就是说,随机效应造成的方差,几乎都等于0。这对于常年通过在自然界摸爬滚打获取数据的生态学者来说,仅凭直觉就能知道,这种结果出现的概率极低,几乎不可能。所以,这个错误很可能是作者对相关模型设置理解不透造成的,而不是纯粹由于粗心大意造成的。
OK,那么我们可以对其模型随机效应结构进行修正如下:
richness.cels.glmmad.poisson2 <- glmmTMB(richness ~
water +
tmax +
last_3_ppt +
(water:tmax)+
(water:last_3_ppt)+
(1|site/numeric_day),
data=all_water.div,
ziformula = ~1,
family=poisson)
然后查看该模型的结果:
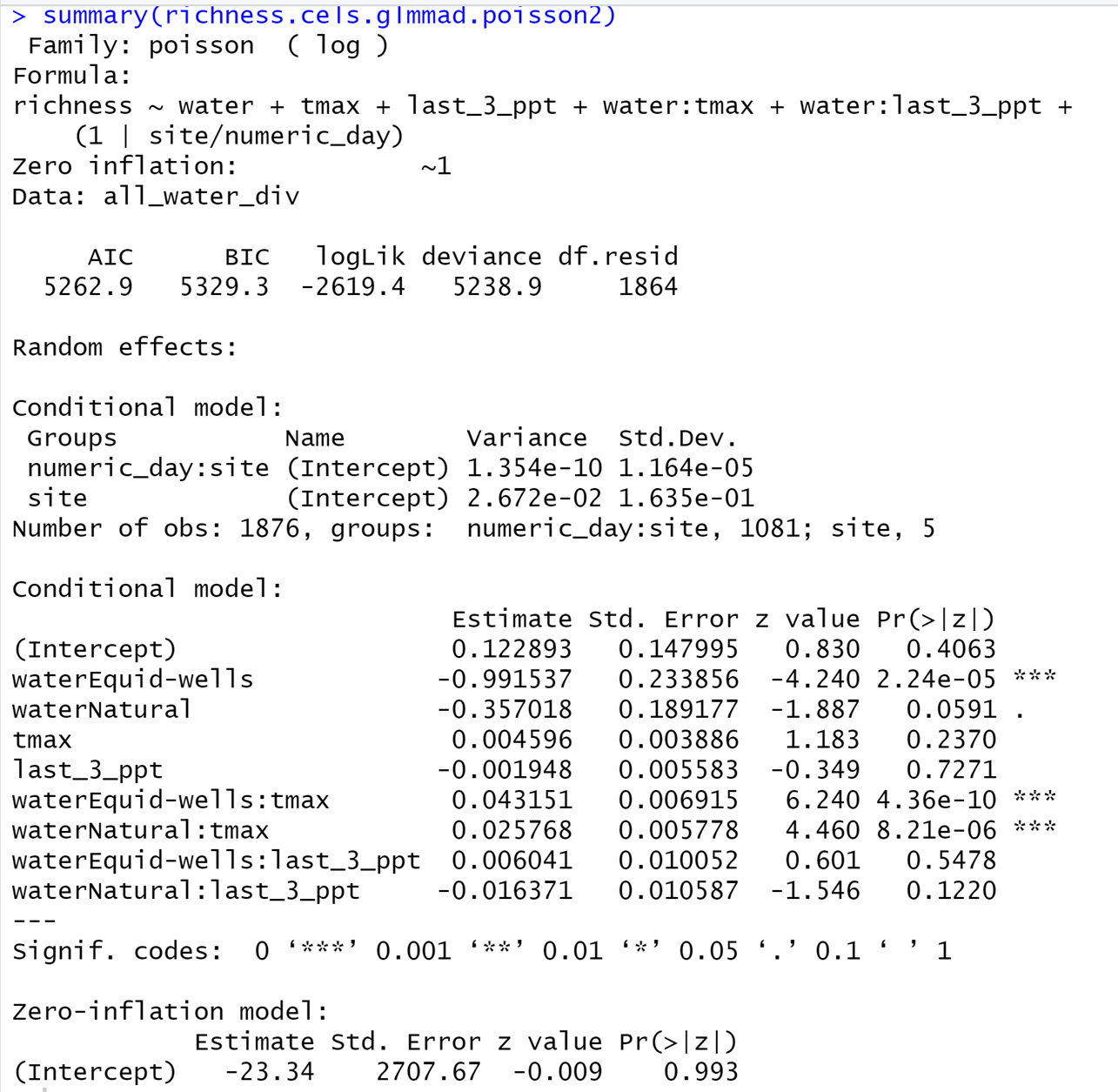
可见,虽然修正后的模型中,固定效应的作用并无本质上的差异,嵌套在site之下的日期造成随机效应依然是10的-10方级。但site造成的随机效应,足足变大了8个数量级(修正后的值为0.0267),二傻哥掐着手指头反复算了算,这竟然是扩大了大约一亿倍。这是什么概念!
也就是说,原模型大大低估了地点之间的差异对来“驴打的井”处吃水的动物的丰富度的影响。当然对于指标控的我们来说,也可以用AIC值对比下两模型的优劣:

可见,自由度不变,修正后模型的AIC值足足比原模型低了50个单位!模型改进之大,只能用铁血丹心来形容。同时,我们也可以比较两模型的R2
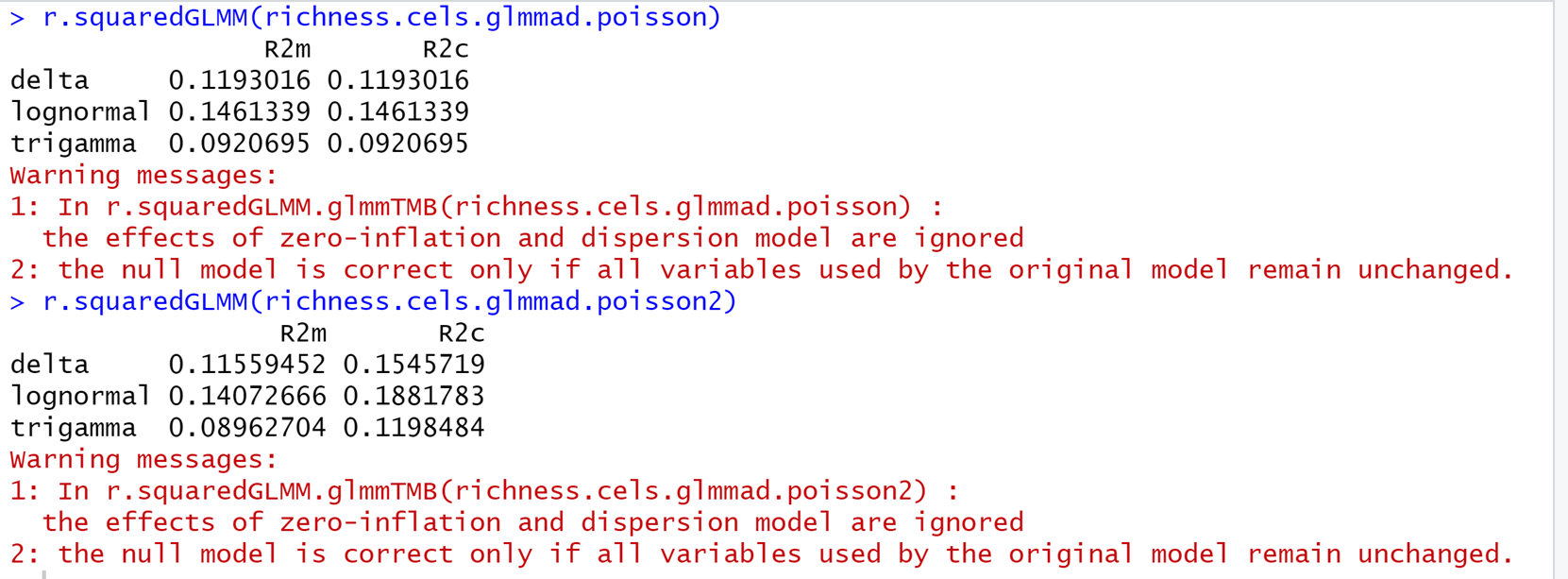
可见,随机效应设置错误模型的模型(红字部分可以忽略),随机效应对R2毫无贡献(conditional R2和marginal R2完全相等),这在对于在野外自然条件下采样的研究,是极不正常的。同样,我们也可以总体上对比下两模型在参数估计上的差异:
par(mar = c(5, 5, 2, 2))
plot(rd1$Estimate, rd2$Estimate,xlab="原模型(嵌套错误)参数估计值", font=2,
ylab="嵌套改正后模型参数估计值",cex.lab=1.5,
pch = 16, cex=1.5, ylim = c(-1,0.5), xlim=c(-1,0.5))
abline(a =0, b = 1, col = "blue")
v1<-1.168e-10
v2<-1.700e-10
v3<-2.672e-02
v4<-2.229e-10
points(x=c(v1,v2), y=c(v3,v4), pch = 16, cex=1.5, col="red")
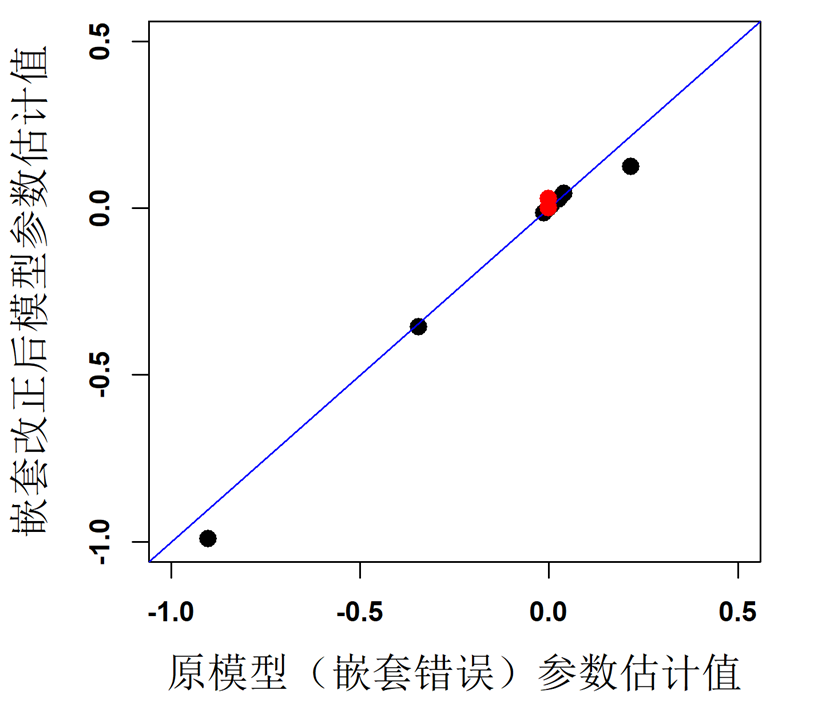
显然,两模型的参数估计值,具有肉眼可见的差异。非常遗憾,不仅仅是这一个模型,这篇论文里所有的嵌套模型设置,都是错误的。这是否对会对其他模型的结果造成本质性影响(仅就本文测试的一模型来讲,并未对固定效应结果产生实质性影响),吃瓜群众们可以自行验证。
最后,众筹科研不易,这里也向论文的作者表示敬意,也向其无私的公开研究数据和分析代码表示感谢!这篇文章也是学习其他统计方法(如混合模型的多重比较)和制图的佳作,也向道友们强烈推荐。
参考文献:
Lundgren, E. J., D. Ramp, J. C. Stromberg, J. Wu, N. C. Nieto, M. Sluk, K. T. Moeller, and A. D. Wallach. 2021. Equids engineer desert water availability. Science 372:491-495.


https://m.sciencenet.cn/blog-3442043-1362371.html
上一篇:两组数据存在方差异质性时的t检验问题
下一篇:从Ecology letters上一篇technical comment 看当前meta分析研究中需要注意的几个技术问