博文
An introduction to Sparse Representation
||||
Preliminaries
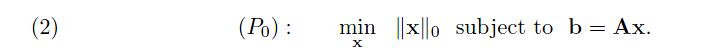
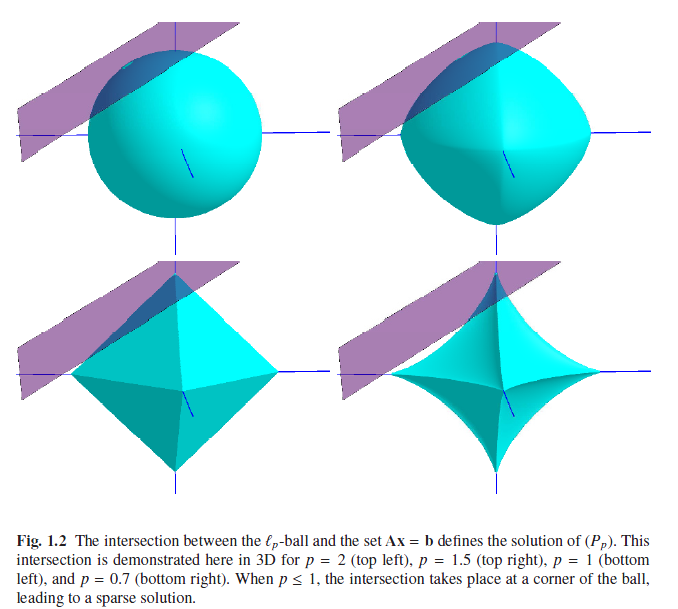
From above figure, only the norm are eque or less than 1,the intersection point is on the axises. so we can present it use only one nonzore.On the other hand, the norm which eque or lager than one can see as an convex optimation problem.
https://m.sciencenet.cn/blog-621576-551052.html
下一篇：Sparse Representation (Cont.)
A full-rank matrix A ∈ Rn×m with n < m generates an underdetermined system of linear equations Ax = b having infinitely many solutions.Suppose we seek the sparsest solution, i.e., the one with the fewest nonzero entries. Can it ever be unique? If so, when? As optimization of sparsity is combinatorial in nature, are there efficient methods for finding the sparsest solution?
Sparse Solutions of Linear Systems of Equations?.
Consider a full-rank matrix A ∈ Rn×m with n < m, and define the underdetermined linear system of equations Ax = b. This system has infinitely many solutions; if one desires to narrow the choice to one well-defined solution, additional criteria are needed. Here is a familiar way to do this. Introduce a function J(x) to evaluate the desirability of a would-be solution x, with smaller values being preferred. Define the general optimization problem (PJ ),
Selecting a strictly convex function J(·) guarantees a unique solution. Take 2 norm mueasurement as an example, this is given explicitly by
Measurement
The vector is sparse,if there are few nonzeros among the possible entries in x. It will be convenient to introduce the 0 “norm”
Thus if x0 m, x is sparse.
Consider the problem (P0) obtained from the general prescription (PJ ) with the choice J(x) = J0(x) ≡ x0; explicitly,
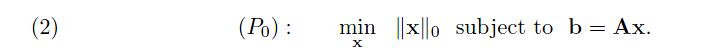
Sparsity optimization (2) looks superficially like the minimum 2-norm problem (P2), but the notational similarity masks some startling differences. The solution to (P2) is always unique and is readily available through now-standard tools from computational linear algebra. (P0) has probably been considered to be a possible goal from time to time for many years, but initially it seems to pose many conceptual
challenges that have inhibited its widespread study and application. These are rooted in the discrete and discontinuous nature of the 0 norm; the standard convex analysis ideas which underpin the analysis of (P2) do not apply. Many of the most basic questions about (P0) seem immune to immediate insight:
• Can uniqueness of a solution be claimed? Under what conditions?
• If a candidate solution is available, can we perform a simple test to verify that the solution is actually the global minimizer of (P0)?
Perhaps, in some instances, with very special matrices A and left-hand sides b, ways to answer such questions are apparent, but for general classes of problem instances (A, b), such insights initially seem unlikely.
From above figure, only the norm are eque or less than 1,the intersection point is on the axises. so we can present it use only one nonzore.On the other hand, the norm which eque or lager than one can see as an convex optimation problem.If 0 norm solution is hard to obtain, we can use 1 norm to be an alternate way.
The proof about the equivalency of zero norm and one norm problem can find in[1].
Two ways to get the sparse solution. 
Two ways to get the sparse solution.
(1) Greedy Algorithm-OMP[2]
(2) Basis Pursuit-IRLS,LARS,Feature-sign search algorithm[3].
Reference:
[1] A. M. Bruckstein, D. L. Donoho, and M. Elad, “From sparse solutions of systems of equations to sparse modeling of signals and images,” SIAM Review, vol. 51, no. 1, pp. 34–81, 2009.
[2] Y.C. Pati, R. Rezaiifar, and P.S. Krishnaprasad, "Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition," in Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Vol. 1, 1993, pp. 40–44.
[3] H. Lee, A. Battle, R. Raina and Andrew Y.Ng, "Efficient sparse coding algorithms" in In NIPS, 2007.
https://m.sciencenet.cn/blog-621576-551052.html
下一篇：Sparse Representation (Cont.)
