Suppose there is a sample x₁, x₂, ..., x_n of n independent and identically distributed observations, coming from a distribution with an unknownprobability density function f₀(·). It is however surmised that the function f₀ belongs to a certain family of distributions { f(·| θ), θ ∈ Θ }, called the parametric model, so that f₀ = f(·| θ₀). The value θ₀ is unknown and is referred to as the true value of the parameter. It is desirable to find an estimator 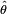 which would be as close to the true value θ₀ as possible. Both the observed variables x_i and the parameter θ can be vectors.

To use the method of maximum likelihood, one first specifies the joint density function for all observations. For an independent and identically distributed sample, this joint density function is

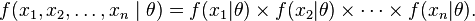
Now we look at this function from a different perspective by considering the observed values x₁, x₂, ..., x_n to be fixed "parameters" of this function, whereas θ will be the function's variable and allowed to vary freely; this function will be called the likelihood:

In practice it is often more convenient to work with the logarithm of the likelihood function, called the log-likelihood:

or the average log-likelihood:

The hat over ℓ indicates that it is akin to some estimator. Indeed, 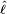 estimates the expected log-likelihood of a single observation in the model.

The method of maximum likelihood estimates θ₀ by finding a value of θ that maximizes 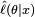. This method of estimation defines a maximum-likelihood estimator (MLE) of θ₀

if any maximum exists. An MLE estimate is the same regardless of whether we maximize the likelihood or the log-likelihood function, since log is a monotonically increasing function.

For many models, a maximum likelihood estimator can be found as an explicit function of the observed data x₁, ..., x_n. For many other models, however, no closed-form solution to the maximization problem is known or available, and an MLE has to be found numerically using optimizationmethods. For some problems, there may be multiple estimates that maximize the likelihood. For other problems, no maximum likelihood estimate exists (meaning that the log-likelihood function increases without attaining the supremum value).

In the exposition above, it is assumed that the data are independent and identically distributed. The method can be applied however to a broader setting, as long as it is possible to write the joint density function f(x₁, ..., x_n | θ), and its parameter θ has a finite dimension which does not depend on the sample size n. In a simpler extension, an allowance can be made for data heterogeneity, so that the joint density is equal tof₁(x₁|θ) · f₂(x₂|θ) · ··· · f_n(x_n | θ). In the more complicated case of time series models, the independence assumption may have to be dropped as well.

A maximum likelihood estimator coincides with the most probable Bayesian estimator given a uniform prior distribution on the parameters.

 

From: http://en.wikipedia.org/wiki/Maximum_likelihood

 

As an example, consider a set C of N Bernoulli experiments with unknown parameter p, e.g., realised by tossing a deformed coin. The Bernoulli density function for the r.v. C for one experiment is:

$p(C=c|p)$=$p^c(1-p)^{1-c}$

where we define c=1 for heads and c=0 for tails.

Building an ML estimator for the parameter p can be done by expressing the (log) likelihood as a function of the data:

 

$\mathcal{L}$=$\log \prod^{N}_{i=1}p(C=c_i)$=$\sum^{N}_{i=1} p(C=c_i|p)$=$n^{(1)} \log p(C=1|p)$ + $n^{(0)} \log p(C=0|p)$ = $n^{(1)}\log p$ + $n^{(0)} \log (1-p)$

 

where $n^{(c)}$ is the number of times a Bernoulli experiment yielded event c. Differentiating with respect to (w.r.t.) the parameter p yields:

 

$\frac{\partial \mathcal{L}}{\partial p} = \frac{n^{(1)}}{p} - \frac{n^{(0)}}{1-p} =0 $

 

$\hat{p}_{ML} = \frac{n^{(1)}}{n^{(0)} + n^{(1)}} = \frac{n^{(1)}}{N} $

 

which is simply the ratio of heads results to the total number of samples. To put some numbers into the example, we could imagine that our coin is strongly deformed, and after 20 trials, we have $n^{(1)}=12$ times heads and $n^{(0)}=8$ times tails. This results in an ML estimation of of $\hat{p}_{ML} = 12=20 = 0.6$.

 

转载本文请联系原作者获取授权，同时请注明本文来自马凤龙科学网博客。
链接地址：https://m.sciencenet.cn/blog-637823-628980.html

上一篇：灰色十月