博文
概率论悖论
 精选
精选
|||
概率论悖论-趣谈概率统计之2
如今,“概率”一词在我们的生活中随处可见,被人们使用得越来越广泛和频繁。这是一个多变的世界,一切都在变化,一切都难以确定。这个世界是由变量构成的,其中包括决定性变量,比如新闻说:“北京时间2016年11月3日20时43分,长征五号在海南文昌成功发射”,这儿的时间地点都是固定的决定性变量。但我们的生活中也有许多随机变量,比如明天雾霾的程度,或百度的股票值,都是不确定的随机变量。随机变量用概率来描述。处处是随机变量,因而处处有概率。你打开电视听天气预报,看看今天会不会下雨?气象预报员告诉你说:今天早上8点钟的“降水概率”是90%。你到手机上查询股市中的某种股票,你得到的信息可能是这种股票3个月之后翻倍的概率是67%。你满怀期望地买了50张彩票,朋友却告诉你,傻瓜才去百花这50块钱,因为你中奖的概率只有一亿分之一!你手臂上长了一个“肉瘤”,医生初步检查后安慰你,这块东西是恶性瘤的概率只有0.03%,万分之三而已!生活中概率这个词太常见了,以至于人们不细想也大概知道是个什么意思,比如说最后一个例子中,0.03%恶性概率的意思不就是说,“10000个这样的肉瘤中,只有3个才会是恶性的”吗。因此,概率就可以被粗糙地定义为事件发生的频率,即发生次数与总次数的比值。更准确地说,是总次数趋于无限时,这个比值趋近的极限。
虽然概率的定义不难懂,好像人人都会用,但你可能不知道,概率计算的结果经常违背我们的直觉,概率论中有许多难以解释、似是而非的悖论。不能完全相信直觉!我们的大脑有它的误区和盲点,就像开汽车的驾驶员视觉中有“盲点”一样,需要几面镜子来帮助克服,我们的思维过程中也有盲点,需要计算和思考来帮助澄清。概率论是一个经常出现与直觉相悖的奇怪结论的领域,连数学家也是稍有不慎便会错得一塌糊涂。现在,我们就来看看经典概率中的几个著名悖论和谬误。
基本比率谬误(base rate fallacy)
先看一个生活中的例子。
王宏去医院作验血实验,检查他患上了X疾病的可能性,其结果居然为阳性,把他吓了一大跳,赶忙到网上查询。网上的资料说,实验总是有误差的,这种实验有“百分之一的假阳性率和百分之一的假阴性率”。这句话的意思是说,在得病的人中做实验,有1%的人是假阳性,99%的人是真阳性。而在未得病的人中做实验,有1%的人是假阴性,99%的人是真阴性。于是,王宏根据这种解释,估计他自己得了X疾病的可能性(即概率)为99%。王宏想,既然只有百分之一的假阳性率,那么,百分之九十九都是真阳性,那我已被感染X病的概率便应该是99%。
可是,医生却告诉他,他被感染的概率只有0.09左右。这是怎么回事呢?王宏的思路误区在哪里?
医生说:“百分之九十九?哪有那么大的感染几率啊。99%是测试的准确性,不是你得病的概率。你忘了一件事:这种X疾病的正常比例是不大的,1000个人中只有一个人有X病。”
医生的计算方法是这样的:因为测试的误报率是1%,1000个人将有10个被报为“假阳性”,而根据X病在人口中的比例(1/1000=0.1%),真阳性只有1个。所以,大约11个测试为阳性的人中只有一个是真阳性(有病)的,因此,王宏被感染的几率是大约1/11,即0.09(9%)。
王宏想来想去仍感糊涂,但这件事激发了王宏去重温他之前学过的概率论。经过反复阅读,再思考琢磨医生的算法之后,他明白了自己是犯了那种叫做“基本比率谬误”的错误,即忘记使用“X病在人口中的基本比例(1/1000)这个事实。
谈到基本比率谬误,我们最好是先从概率论中著名的贝叶斯定理【1】说起。托马斯·贝叶斯(ThomasBayes ,1701年–1761年)是英国统计学家,曾经是个牧师。贝叶斯定理是他对概率论和统计学作出的最大贡献,是当今人工智能中常用的机器学习之基础框架,它的思想之深刻远出一般人所能认知,也许贝叶斯自己生前对此也认识不足。因为如此重要的成果,他生前却并未发表,是他死后的1763年,才由朋友发表的。本篇将对贝叶斯定理稍作介绍,我们在本系列的后几篇,将讨论贝叶斯学派以及贝叶斯理论在人工智能中的应用。
初略地说,贝叶斯定理涉及到两个随机变量A和B的相互影响,如果用一句话来概括,这个定理说的是:利用B带来的新信息,应如何修改B不存在时A的“先验概率”P(A),从而得到B存在时的“条件概率”P(A|B),或称后验概率,如果写成公式便是:
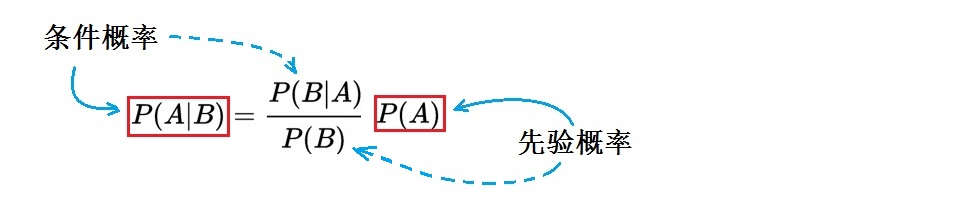
这儿“先验后验”的定义是一种“约定俗成”,是相对的。比如说也可以将A、B反过来叙述,即如何从B的“先验概率”P(B),得到B的“条件概率”P(B|A),见图中虚线所指。
不要害怕公式,通过例子,我们能慢慢理解它。例如,对前面王宏看病的例子,随机变量A表示“王宏得X病”;随机变量B表示“王宏检查结果”。先验概率P(A)指的是王宏没有检查结果时得X病的概率(即X病在公众的基本概率0.1%),而条件概率(或后验概率)P(A|B)指的是王宏“检查结果为阳性”的条件下得X病的概率(9%)。如何从基本概率修正到后验概率的?待会儿再解释。
贝叶斯定理是18世纪的产物,200来年用得好好的,不想在20世纪70年代遇到了挑战,该挑战来自于卡尼曼和特维尔斯基(Tversky)提出的“基础概率谬误”(Base-RateFallacy)。丹尼尔·卡尼曼(Daniel Kahneman,1934年-)是以色列裔美国心理学家,2002年诺贝尔经济学奖得主。基础概率谬误并不是否定贝叶斯定理,而是探讨一个使人困惑的问题:为什么人的直觉经常与贝叶斯公式计算的结果相违背?如同刚才的例子所示,人们在使用直觉的时候经常会忽略基础概率。卡尼曼等在他的文章《思考,快与慢》中举了一个出租车的例子来启发人们思考这个影响人们“决策”的原因。我们不想在这儿深谈基础概率谬误对“决策理论”的意义,只是借用此例来加深对贝叶斯公式的理解:
某城市有两种颜色的出租车:蓝和绿(市场比率15:85)。一辆出租车夜间肇事后逃逸,但还好当时有一位目击证人,这位目击者认定肇事的出租车是蓝色的。但是,他“目击的可信度”如何呢?公安人员经过在相同环境下对该目击者进行“蓝绿”测试而得到:80%的情况下识别正确,20%的情况不正确。也许有读者立刻就得出了结论:肇事之车是蓝色的几率应该是80%吧。如果你作此回答,你便是犯了与上面例子中王宏同样的错误,忽略了先验概率,没有考虑在这个城市中“蓝绿”车的基本比例。
那么,肇事之车是蓝色的(条件)几率到底应该是多少呢?贝叶斯公式能给出正确的答案。首先我们必须考虑蓝绿出租车的基本比例(15: 85)。也就是说,在没有目击证人的情况下,肇事之车是蓝色的几率只有15%,这是“A=蓝车肇事”的先验概率P(A)= 15%。现在,有了一位目击者,便改变了事件A出现的概率。目击者看到车是“蓝”色的。不过,他的目击能力也要打折扣,只有80%的准确率,即也是一个随机事件(记为B)。我们的问题是要求出在有该目击证人“看到蓝车”的条件下肇事车“真正是蓝色”的概率,即条件概率P(A|B)。后者应该大于先验概率15%,因为目击者看到“蓝车”。如何修正先验概率?为此需要计算P(B|A)和P(B)。
因为A=车为蓝色、B=目击蓝色,所以P(B|A)是在“车为蓝色”的条件下“目击蓝色”的概率,即P(B|A)=80%。最后还要算先验概率P(B),它的计算麻烦一点。P(B)指的是目击证人看到一辆车为蓝色的概率,等于两种情况的概率相加:一种是车为蓝,辨认也正确;另一种是车为绿,错看成蓝。所以:
P(B) = 15%×80% + 85%×20% = 29%
从贝叶斯公式:
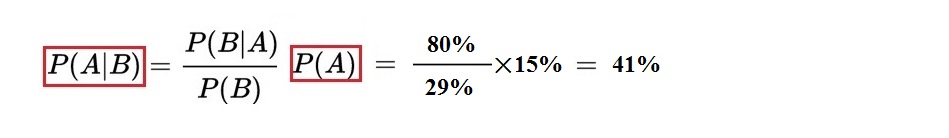
可以算出在有目击证人情况下肇事车辆是蓝色的几率=41%,同时也可求得肇事车辆是绿车的概率为59%。被修正后的“肇事车辆为蓝色”的条件概率41%大于先验概率15%很多,但是仍然小于肇事车可能为绿的概率0.59。对王宏测试X病的例子,读者可以参考这儿的方法,不难得出正确的答案,作者就不再赘述了。

几何概型和贝特朗悖论【2】
抛硬币、掷骰子之类游戏中涉及的概率,是离散的,抛丢结果的数目有限(2或6)。如果硬币或骰子是对称的,每个基本结果发生的概率相等。这种随机事件被称为古典概型。数学家们将古典概型推广到某些几何问题中,使得随机变量的结果变成了连续的,数目成为了无限多,这种随机事件被称之为“几何概型”。古典概型向几何概型的推广,类似于有限多个整数向“实数域”的推广。了解几何概型很重要,因为与之相关的“测度”概念(长度、面积等),是现代概率论的基础。
布封投針问题,是第一个被研究的几何概型。
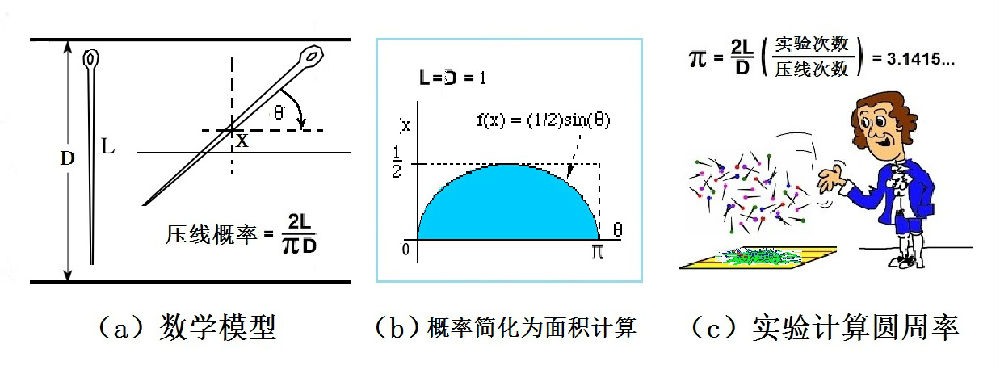
图1:布封(Buffon)投針问题
18世纪的法国,有一个著名的博物学家:乔治·布丰伯爵(George Buffon,1707-1788年)。他研究不同地区相似环境中的各种生物族群,也研究过人和猿的相似之处,以及两者来自同一个祖先的可能性,他的作品对现代生态学影响深远,他的思想对达尔文创建进化论影响很大。
难得的是,布丰同时也是一位数学家,是最早将微积分引入概率论的人之一。他提出的布封投針问题(图1)是这样问的:
用一根长度为L的針,随机地投向相隔为D的平行线(L < D),针压到线的概率是多少?
布封投针问题中,求的也是概率,但这时投掷的不是硬币或骰子,而是一根针。硬币投下去只有“正反”两种基本结果,对公平硬币而言,每种概率1/2。公平骰子有6种结果,每一个面出现概率为1/6。我们现在分析一下布封投针的结果。按照图1a所示的数学模型,投针投下之后的状态可以用两个随机变量来描述,针的中点的位置x,以及针与水平方向所成的角度q。x在-D/2到D/2之间变化,q在0到2π间变化。因为x和q的变化是连续的,所以其结果有无限多。古典概率中的求和在几何概率中用积分代替,使用积分的方法不难求出布封探针压线的几率为2L/(Dπ)。
因为布封投针中的概率是对于x和q的2维积分,所以概率的计算可以简化为如图1b所示的几何图形的面积计算,即所求概率等于图1b中阴影面积与矩形面积之比。
布封投针的结果提供了一个用概率实验来确定圆周率π的方法(蒙特·卡罗法)。因为π=2L/(DP),当针投掷的次数足够大,得到的概率P足够精确时,便可以用以上公式计算π。的确有些出乎意料之外,真没想到用一根针丢来丢去也能丢出一个数学常数来!
从上面的介绍可知,几何概型将古典概型中的离散随机变量扩展到了连续随机变量,求和变成积分,变量的样本空间从离散和有限扩展到无穷。几何概型和古典概型都使用“等概率假设”。然而,只要涉及到无穷大,便经常会产生一些怪异的结果。布封投针问题中条件清楚,没有引起什么悖论,著名的几何概型悖论是法国学者贝特朗(Joseph Bertrand,1822–1900)于1889年提出的贝特朗悖论。
贝特朗提出的问题是:在圆内任作一弦,求其长度超过圆内接正三角形边长L的概率。奇怪之处在于,这个问题可以有三种不同的解答,结果完全不同但听起来却似乎都有道理。

图2:贝特朗悖论
求解贝特朗问题中的概率,不需要用微积分,只需要利用几何图形的对称性便能得到答案。与计算布封投针问题中概率的情况类似(图1b),一般来说,可以将几何概率的计算变换成几何图形的计算,即计算弧长或线段的长度,或者是面积或体积,从如下计算贝特朗问题的3种不同方法,读者可以更为深入地理解这点。
方法1:首先假设弦的一端固定在圆上某一点(比如A),如图2a,弦的另一端在圆周上移动。移动端点落在弧BC上的弦,长度均超过圆内接正三角形的边长L,而其余弦的长度都小于L。由于对称性,BC弧长占整个圆周的1/3,所以可得弦长大于L的概率为BC弧长与圆周长之比,即P=1/3。
方法2:首先选择圆的一个直径,比如图2b中的AD。过该直径上的任何点作直径的垂线,与圆相交形成弦。从图2b中可以看出:当直径上动点的位置在B和C之间时,所得弦的弦长大于正三角形的边长L,动点位置在BC之外的弦长小于L。因为线段BC的长度是整个直径的一半,所以由此可得弦长大于L的概率为P=1/2。
方法3:如图2c所示,作一个半径只有圆的半径的二分之一的同心圆(称为小圆),称原来的圆为“大圆”。考虑大园上任意弦的中点的位置可知:当中点位于小圆内部时,弦长符合大于L的要求。因为小圆的面积是大圆面积的1/4。所以,概率也为P=1/4。
以上3种方法听起来都振振有辞,但得出不同的结果,是怎么回事呢?
按照传统解释,关键在于“随机”选择弦的方法。方法不同,“等概率假设”的应用区间也不一样。方法1假定端点在圆周上均匀分布(即等概率);方法2假定弦的中点在直径上均匀分布;方法3则假定弦的中点在圆内均匀分布,图3给出了3种解法中弦的中点在园内的分布情形。图4则是用3种方法直接画出弦,以比较弦在园内的分布情形。也可以说,贝特朗悖论不是悖论,只是问题中没有明确规定随机选择的方法,方法一旦定好了,问题自然也就有了确定的答案。

图3:弦的“中点”在3种方法中的分布情况

图4:“弦”在3种方法中的分布情况
本篇前部分通过介绍初等概率论中的几个悖论,我们初步了解了十分重要的贝叶斯定理及其应用,后半部分则认识了几何概型。概率论中悖论很多,基于经验的直觉判断很多时候往往并不靠谱。下一篇将要介绍的本福特定律,也是一条初看起来有些奇怪、不合直觉的定律,不过这条定律用处挺大,甚至还能帮助侦破“财务造假”,且听下回分解。
王宏检查问题的补充和修正:

有关贝叶斯,科学网上2013年,就有一篇很好的科普文章:
http://blog.sciencenet.cn/blog-103568-707316.html
参考资料:
【1】维基百科-贝叶斯定理:https://zh.wikipedia.org/wiki/%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%AE%9A%E7%90%86
【2】wikipidia:Bertrand_paradox_(probability)
https://en.wikipedia.org/wiki/Bertrand_paradox_(probability)
本文同步发表在“知识分子”微信公众平台上
概率问题与贝叶斯定理
https://m.sciencenet.cn/blog-677221-1042909.html
上一篇:上帝教人掷骰子-“神童”帕斯卡与概率论
下一篇:浅谈分布之分布(beta分布)-贝叶斯分析之1