博文
浅谈量子计算机-3
 精选
精选
||
**** 4. 算法 ****
4.1 Grover 量子搜索算法
为什么需要量子算法?因为经典算法不足以体现量子计算特别之处。量子算法的目的便是要利用量子比特量子门的特殊性:叠加性、干涉性、纠缠性……,构造比经典计算快得多的算法。此外,量子算法也需考虑物理可实现性。

图4.1:量子算法发展史
在考虑量子算法时,特别需要关注量子计算的如下特点:
1,量子比特是量子叠加态,几个本征态按不同的概率幅叠加起来;
2,量子计算可以平行计算(或者说对叠加态进行某种“操作”),但是不能测量。因为一旦测量就将导致系统的“波函数塌缩”,即叠加态以一定的概率塌缩到某个本征态,塌缩概率是该本征态概率幅的平方。
Grover量子搜索算法【6】展示量子计算机解决“非结构化搜索问题”的速度可以比经典更快。
给你一个很大的N个项目列表,其中有一项w是我们希望找到的。或者用一个最简单的比喻,假设我们是要在许多嫌疑人中搜索一个逃犯,w表示的就是逃犯。
考虑最简单的情况:N个嫌疑人x中只有一个罪犯w,如图4.2a所示。首先将列表中的每个候选者标以特定颜色,逃犯w为红色,所有其他人x都标以灰色。规定某种方法判定逃犯,例如考虑一个与“计算”有关的方法:假设我们知道罪犯的身份证号码w,可将它与所有嫌疑人的号码x比较,即做减法计算(x-w)。结果则可以用一个二元目标检验函数f(x)表示:如果x不等于w,f(x)=0;如果x是逃犯,即x= w,f(x)=1。因为嫌疑人的数据x是无序的,如果使用经典方法,要找到逃犯的号码w,只能一个一个地做减法。最坏情况需检查所有N个嫌疑人,最好情况也得检查1个,平均而言必须做N/2次减法。因此,经典搜索的运算次数与N的关系是线性的:O(N)。
现在考虑量子搜索,假设“数据库”由量子比特可能处于的所有计算基组成。例如 3 个量子比特,如图4.2b所示,计算基列表就是:|000>, |001>,……|111>,即从0 到7八个值,量子搜索可以同时操作这8个寄存器。但是,一开始我们并不知道要找的逃犯w在哪里,所有的嫌疑人都有可能是罪犯。因此,似乎我们也只能一个一个地计算验证!如果那样的话,仍然需要和经典情况一样的线性复杂度N,体现不了量子运算的优越性。
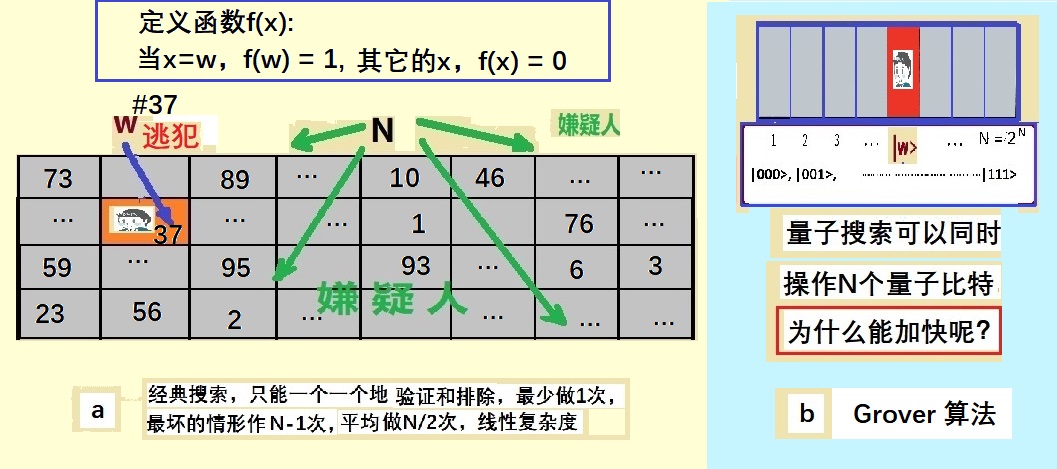
图4.2:搜索问题和检验函数f(x)
既然均等概率体现不了量子计算的特点,就想办法让概率变化。Grover算法就是非常巧妙地利用了量子计算机可以“平行运算”的特点,同时对N个寄存器反复进行某种操作,使得目标项w的概率幅|w>不断放大,其他的概率幅|x>不断缩小,这种算法可以只用sqrt(N) 个步骤找到罪犯w。比较经典计算需要的N步,得到了平方级的加速。
听起来增速不多,仅仅平方级的加速。但实际上是我们所能期望的搜索算法最大加速。 并且当N很大时,二次加速确实可以节省大量时间。比如有100个嫌疑人,身份证号码1到100,随机无序地分布在100个寄存器中,找出数字37的所在之处,经典方法需要平均做50次操作,量子方法只需要做10次!N越大,加速越明显。此外,该算法的用途不止于数据搜索,具有通用性,可以为各种其他算法获得二次运行的时间改进。
Grover 算法的核心就是振幅放大技巧,将目标w的概率幅放大,而将其它“非目标项”x的概率幅缩小。振幅放大过程分两步:量子黑箱函数Uw(也称Quantum Oracle),和扩散算符操作Us(Diffusion Operator)。

图4.3:振幅放大的几何解释
“振幅放大”算法有很好的几何解释,表示为态矢量在一个二维平面中产生旋转,如图4.3所示。初始状态是一个均匀叠加态|s> ,|w>和|s>张成向量空间中的一个二维平面,两个向量|w>和|s>并不完全垂直,因为|w>也以N1/2的概率辐出现在叠加态|s>中。然而,我们可以引入一个额外的状态|s‘>,它位于|w>和|s>构成的二维平面上但垂直于|w> 。
更详细地分几步说明:刚才的初始态算是步骤 1 ,振幅放大过程从均匀叠加|s>开始,均匀叠加态|s>可以很容易地从n个H门作用于n个量子比特基态|0>上构造出来,得到如图4.3左图所示的初始状态。在|w>和|s‘>构成的平面坐标下,初始状态|s>可以表示为:
|s> = sinT |w> + cosT |s‘>,
角T = arcsin(s在w的投影) = arcsin(1/ N1/2),图4.3左下图形是均匀叠加态|s>的bar图。
步骤 2,应用黑箱函数Uw将状态|s>翻转,见图4.3的中图:Uw的作用是将目标状态|w>反相,其它状态不变。从几何上讲,这对应于|s>态关于|s‘>轴的翻转。这意味着状态|s>中|w>的幅度变为负值,也意味着平均幅度(由虚线表示)的降低。
步骤3,现在关于状态|s>应用另一个扩散算符Us。此转换将|s>映射到状态UsUw|s>。两次反射Us和Uw对应一个旋转,将初始状态|s>旋转得更接近|w>,见图4.3右图。
幅度条形图中Us的反射操作可以理解为关于平均幅度(虚线)的反射。由于第一次反射降低了平均振幅,这变换将|w>的振幅提高到其原值的数倍,同时也降低了其他振幅,故称为振幅放大。
然后我们转到前面重复步骤 2和步骤3,继续振幅放大的过程直到达到要求。
图4.3所示的过程的确可将振幅放大,但到此为止我们有两个问题:一是图中的黑箱函数Uw和扩散算符Us具体是什么?二是此过程要重复几次才能找到w呢?
Grover 算法的预言机Oracle函数Uw所做的,是给解|w>添加了一个负相位,也就是说,对于计算基中的任何状态|x>,可以创建一个函数 Uw:Uw (x) = x,如果|x>不等于|w>;而Uw (x) = -x,如果|x>等于|w>,如图4.4a所示。该函数被称为Oracle。
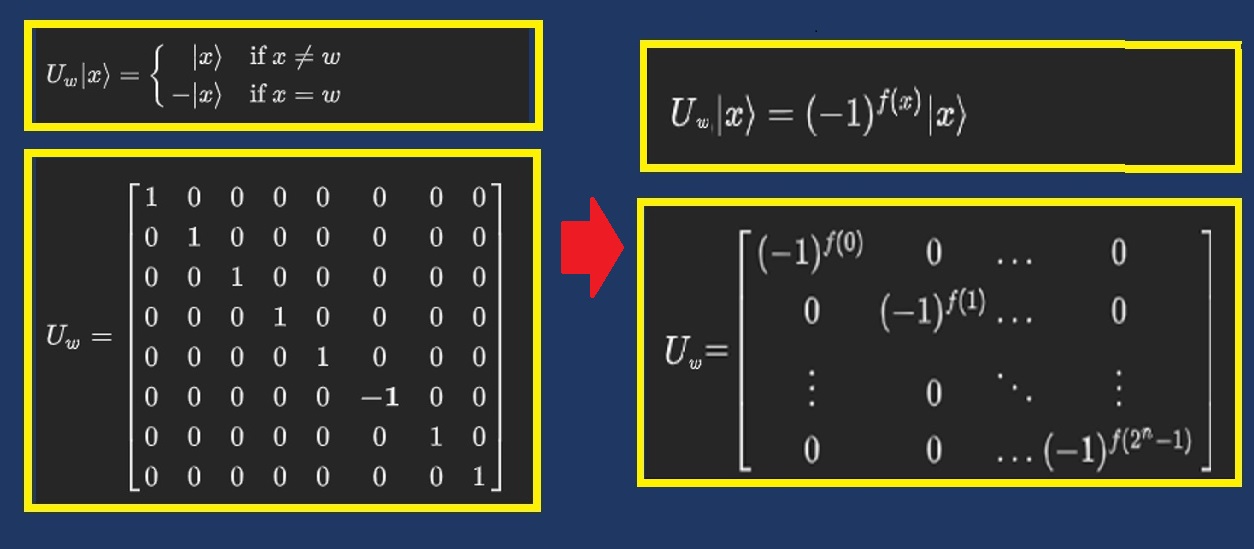
图4.4:a)黑箱函数将w反相;b)相位黑箱函数
图17a中,黑箱函数Uw可以表达为一个对角矩阵,其中对应于目标项w的值为-1,其它为1。图4.4a下图表示三个量子位 的Uw矩阵。进一步具体而言,Oracle可以用图4.2b中所示的经典检验函数f(x)构成的相位函数来实现。
也许有人会说,既然Uw可以将w那一项反相,不是已经知道了w的位置吗?那还搜索什么呢?这是初学Grover算法时经常感觉困惑的问题。这儿需要再次强调量子计算的特点:可以让多个寄存器同时运算但不能检查每个寄存器的结果。因此,虽然我们说Uw能够将w反号,但因为没有进行测量,我们并不知道是哪个寄存器的结果反相了。反相的结果是每个寄存器根据它自己内部的数据检验f(x)而反馈回来的。
换句话说,每个嫌疑人自己知道他是不是罪犯,但我们并不知道,除非进行测量!
即使进行测量,仅仅是将|w>反号这一个操作,也不能确定w的位置。因为|w>是概率辐,而测量得到的是概率,即概率辐的平方。|w>符号的改变使概率辐反相,但并不会影响概率。Grover算法的巧妙之处是在步骤3中我们又应用了一个扩散函数Us = 2 |s><s|-1。其作用是将态矢量关于平均幅度进行反射,反射后w的概率幅被放大了。因此,步骤2和3的共同作用U= UwUs,使得测量后塌缩到|w>的概率被放大了。
那么,现在回到第二个问题:此过程U要重复多少次才能使w的概率幅达到最大值呢?
每一步过程U,都使态矢量的位置更接近|w>的位置,假设每次改变的角度是均匀的2
q,对初始态|s>作用t次之后:|yt> = (UwUf)t|s>。最后需要的次数可用图4.6的描述来粗略地理解。
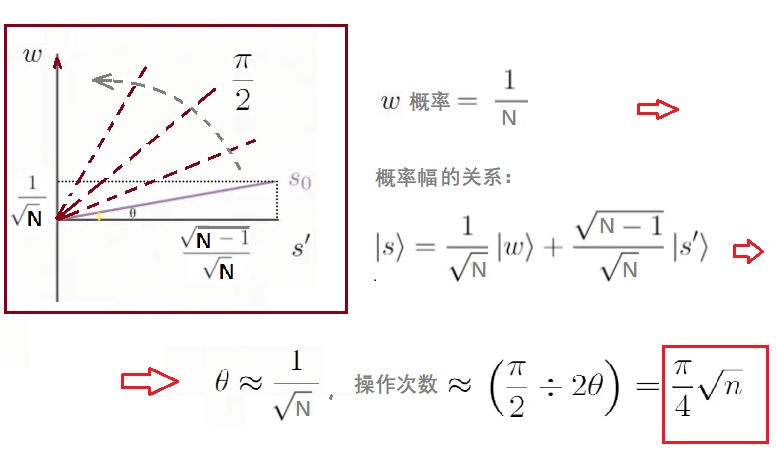
图4.5:Grover算法
事实也证明旋转N^1/2次就足够了。 能从经典的N次减到N^1/2次,原因是由于处理的是概率辐而不是概率,即被放大的是概率幅而不仅是概率,这也是量子计算秘诀所在。
图4.6所示的是用IBM量子模拟的2量子比特搜索过程。经典需要3次比较,量子Grover算法只需要1次。

图4.6:搜索算法举例
参考文献:
【1】Keynote talk, 1st conference on Physics and Computation, MIT, 1981。(International Journal of Theoretical Physics, 21: 467–488, 1982)
【2】Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein; 殷建平等译. 第1章 算法在计算机中的作用. 算法导论 原书第3版. 北京: 机械工业出版社. 2013年1月
【3】张天蓉. 世纪幽灵-走近量子纠缠(第二版)[M].合肥:中国科技大学出版社,2020年5月。
【4】Bloch Sphere(wikipedia),https://en.wikipedia.org/wiki/Bloch_sphere
【5】IBM Quantum (2022). estimator primitive (Version x.y.z) [computer software]. https://quantum-computing.ibm.com/
【6】Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212
相关视频:
(待续)
Contents
**** 1. 前言 ****
**** 2. 历史 ****
**** 3. 基础 ****
3.1 叠加态
3.2 量子比特
3.3 量子门
3.4 量子电路
**** 4. 算法 ****
4.1 Grover 量子搜索算法
4.2 多伊奇算法
4.3 秀尔算法-1(经典,数论部分)
4.4 秀尔算法-2(量子部分)
**** 5. 实现 ****
**********************************************************
作者部分YouTube视频:
https://www.youtube.com/watch?v=0I8FdazqAvc&list=PL6YHSDB0mjBKB2LBZDKL9UhcMMx6GtOsx
https://www.youtube.com/watch?v=_d0wquZkOYU&list=PL6YHSDB0mjBJ6qgfin-xKmP3FtTQr4x7i
*********************************************************
https://m.sciencenet.cn/blog-677221-1413177.html
上一篇:浅谈量子计算机-2
下一篇:浅谈量子计算机-4

