博文
《经典力学》札记: 33(怎么记向量的点乘和叉乘运算)
 精选
精选
|
《经典力学》札记: 33(怎么记向量的点乘和叉乘运算)
龚明,中国科学技术大学
在经典力学、电动力学、流体力学、材料力学等领域,我们经常需要对矢量做运算,其中主要是点乘和叉乘,以及它们的某些导数运算。很多人知道这些公式有表可查,也就懒得去记了。在研究生面试的时候,我也问过学生几次,没有一个人回答出来,后来也就不再问这样的问题了。尽管这样做无可厚非,但如果把它们简单理解为公式表来查询,而不对这些结果加以认识,是会影响到对一些重要概念的理解的。本文总结这些基本的运算的方法,并利用构造法以及特殊函数/数值的方法对每个公式的具体形式给出一个简单、直观的理解。这个方法可以用来处理更加复杂的向量运算问题。
为了方便,我们定义\begin{equation*} {\bf a} = (a_x, a_y, a_z), \nabla = (\partial_x, \partial_y, \partial_z). \end{equation*}也就是说所有粗体符号都是向量,$\nabla$是一个空间导数的向量。在推导过程中,下面的几个结论非常重要,其中$\pm$符号待定(注意一般情况下不会出现其它系数,我们此处排除零)。
第一个结论:假设两个矢量${\bf a}$和${\bf b}$,如果由点乘和叉乘构成一个标量,它只能是$x = \pm {\bf a} \cdot {\bf b}$;
第二个结论:假设两个矢量${\bf a}$和${\bf b}$,如果要由点乘和叉乘构成一个矢量,它只能是${\bf x} = \pm {\bf a} \times {\bf b}$。
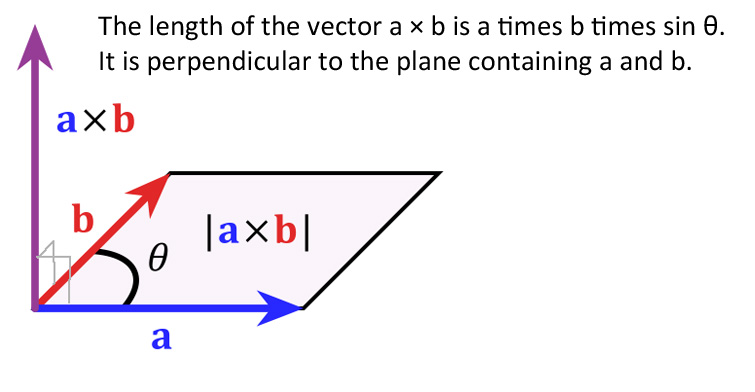
图片来自网络:两个矢量的乘法
${\bf a} \times {\bf b} = -{\bf b} \times {\bf a}$,矢量交换顺序,给出负号,它的值的大小表示面积。如果${\bf a} // {\bf b}$,面积为零,所以其值为零。这个矢量的方向垂直于${\bf a}$和${\bf b}$(见上图)。如果我们展开,应该得到\begin{equation*}{\bf a} \times {\bf b} = (a_y b_z - a_zb_y) i + (a_z b_x - a_x b_z) j + (a_x b_y - a_y b_x) k.\end{equation*}之所以是减号,因为如果${\bf a} = {\bf b}$,它应该为零;如果是加号,就不满足这个条件了。这个方法在下面的例子中会反复用到。
$V = {\bf a} \cdot ({\bf b} \times {\bf c}) = {\bf b} \cdot ({\bf c} \times {\bf a}) = {\bf c} \cdot ({\bf a} \times {\bf b})$, 它表示体积。如果三个矢量是共面的(线性相关的),那么体积为零;否则不为零(线性无关)。利用${\bf a} \times {\bf b} \perp {\bf a}$,${\bf a} \times {\bf b} \perp {\bf b}$,得到$V = {\bf a} \cdot ({\bf b} \times {\bf a}) = 0$。
${\bf a} \times ({\bf b} \times {\bf c})$是一个矢量,它垂直于${\bf a}$的方向,这样我们可以假设\begin{equation*}{\bf a} \times ({\bf b} \times {\bf c}) =x_1 {\bf a} + x_2 {\bf b} + x_3 {\bf c}. \end{equation*}我们需要确定$x_i$的值。考虑$x_1 {\bf a}$, 因为这个向量由${\bf a}$, ${\bf b}$和${\bf c}$构成,因此$x_1$只可能和${\bf b}$和${\bf c}$有关。由这两个矢量构成的标量只能是$x_1 = \eta_1 {\bf b} \cdot {\bf c}$(见上面的结论一)。类似的,我们可以用于$x_2 = \eta_2 {\bf a} \cdot {\bf c}$, $x_3 = \eta_3 {\bf a} \cdot {\bf b}$,其中$\eta_i = 0, \pm 1$。接下来我们要确定它们的符号。如果我们取${\bf b}={\bf c}$,对任意${\bf a}$这个表达式为零,所以有\begin{equation*} 0 = \eta_1 {\bf b}^2 {\bf a} + \eta_2 {\bf a} \cdot {\bf b} {\bf b} + \eta_3 {\bf a} \cdot {\bf b} {\bf b}. \end{equation*} 这个结果表明,$\eta_1 = 0$, $\eta_2 = - \eta_3 = \pm 1$。所以我们猜测其表达式为\begin{equation*} {\bf a} \times ({\bf b} \times {\bf c}) = \eta ({\bf a} \cdot {\bf b} {\bf c} - {\bf a} \cdot {\bf c} {\bf b}). \end{equation*} 之所以没有${\bf a}$的项,是因为这个表达式应该垂直于${\bf a}$。为了确定这个符号,我们可以选择一个特殊的值,比如$a= i$, $b=i$, $c = j$,那么${\bf a} \times ({\bf b} \times {\bf c}) = i \times k = -j$,所以有$\eta = -1$。这样我们得到\begin{equation*} {\bf a} \times ({\bf b} \times {\bf c}) = - {\bf a} \cdot {\bf b} {\bf c} + {\bf a} \cdot {\bf c} {\bf b}. \end{equation*}
$\nabla {\bf v} \cdot (\boldsymbol{\omega} \times {\bf r})$是一个矢量。我们注意到${\bf v} \cdot (\boldsymbol{\omega} \times {\bf r})$是一个标量, 对${\bf r}$求导数得到一个矢量。这个矢量只和${\bf v}$和$\boldsymbol{\omega}$有关,所以我们可以得到\begin{equation*} \nabla {\bf v} \cdot (\boldsymbol{\omega} \times {\bf r}) = \eta {\bf v} \times \boldsymbol{\omega}. \end{equation*}接下来的任务是确定系数的符号。我们可以选择一个特殊值,比如取${\bf v} = (1,0,0) = i$, $\boldsymbol{\omega} = (0,0,1) = k$,那么直接计算得到$\nabla {\bf v} \cdot (\boldsymbol{\omega} \times {\bf r}) = (1,0,0)$,代入上面的公式,考虑到$i\times k = -j$,我们立即得到$\eta = 1$。当然这个结果有一个更加直观的证明,利用体积轮换公式${\bf v} \cdot (\boldsymbol{\omega} \times {\bf r}) = {\bf r} \cdot ({\bf v} \times \boldsymbol{\omega})$,对${\bf r}$求导数,就得到了上面的结论。因此,\begin{equation*} \nabla {\bf v} \cdot (\boldsymbol{\omega} \times {\bf r}) = {\bf v} \times \boldsymbol{\omega}. \end{equation*}这个表达式在经典力学中对应非惯性系中的科里奥利力。
$\nabla (\boldsymbol{\omega} \times {\bf r})^2$是一个矢量,因为我们对${\bf r}$求导数,所以这个矢量只可能有2个$\boldsymbol{\omega}$和一个${\bf r}$构成。那么它可能的形式是\begin{equation*}\nabla (\boldsymbol{\omega} \times {\bf r})^2 = \eta_1 \boldsymbol{\omega} \cdot \boldsymbol{\omega} {\bf r} + \eta_2 \boldsymbol{\omega} \cdot {\bf r} \boldsymbol{\omega}. \end{equation*} 如果我们令$\boldsymbol{\omega} = {\bf r}$,这个表达式为零,所以$\eta_1$和$\eta_2$的符号应该相反。进一步代入一个具体的表达式可以证明,\begin{equation*}\nabla (\boldsymbol{\omega} \times {\bf r})^2 = \boldsymbol{\omega} \times (\boldsymbol{\omega} \times {\bf r}).\end{equation*}这个表达式在经典力学中就是圆周运动的离心力。
$\nabla (fg)$,其中$f$和$g$都是标量,我们要得到一个矢量,而这个矢量只可能有$\nabla f$以及$\nabla g$得到,所以我们猜测\begin{equation*} \nabla (fg) = \eta_1 g \nabla f + \eta_2 f \nabla g.\end{equation*}取$f =g$,这个结果不为零,所以$\eta_1 = \eta_2$必须为相同的符号。同时可以证明$\nabla (f^2) =2f \nabla f$,所以有\begin{equation*} \nabla (fg) = g \nabla f + f \nabla g. \end{equation*}
$\nabla \cdot ({\bf a} \times {\bf b})$,我们要求一个矢量的散度,得到一个标量,而这个标量必须由一些矢量点乘才能得到。这些矢量包括$\nabla \times {\bf a}$, $\nabla \times {\bf b}$, 以及${\bf a}$和${\bf b}$四个,因此我们猜测\begin{equation*} \nabla \cdot ({\bf a} \times {\bf b}) = \eta_1 {\bf a} \cdot \nabla \times {\bf b} + \eta_2 {\bf b} \cdot \nabla \times {\bf a}. \end{equation*} 如果${\bf a} = {\bf b}$,上面的表达式为零,所以$\eta_1 = -\eta_2$。最后假设${\bf a } = i$, ${\bf b} = zj$,那么${\bf a} \times {\bf b} = zk$,所以得到$1 = \eta_1 (-1)$, 我们有\begin{equation*} \nabla \cdot ({\bf a} \times {\bf b}) =- {\bf a} \cdot \nabla \times {\bf b} + {\bf b} \cdot \nabla \times {\bf a}. \end{equation*}
$\nabla \cdot f{\bf a}$,其中$f$是标量,${\bf a}$是矢量,我们希望由它们构造一个标量。这样我们可以猜测\begin{equation*} \nabla \cdot f{\bf a} = \eta_1 f \nabla \cdot {\bf a} + \eta_2 (\nabla f) \cdot {\bf a}. \end{equation*}其中系数只能为$\pm 1$。如果$f$是一个和位置无关的常数,那么只有第一项,显然有$\eta_1 = 1$。如果取${\bf a}$和位置无关的常数,那么只有第二项,也可以证明$\eta_2 = 1$,所以上面的表达式应该为\begin{equation*} \nabla \cdot f{\bf a} =f \nabla \cdot {\bf a} + (\nabla f) \cdot {\bf a}. \end{equation*}
$\nabla \times {\bf a}\times {\bf b}$,我们希望构造一个矢量。利用所有可能的矢量,我们猜测下面的一个复杂的形式\begin{equation*}\nabla \times {\bf a}\times {\bf b} =\eta_1 (\nabla \cdot {\bf a}) {\bf b} + \eta_2 (\nabla \cdot {\bf b}) {\bf a} + \eta_3 (\nabla \times {\bf a}) \times {\bf b} + \eta_4 (\nabla \times {\bf b}) \times {\bf a}. \end{equation*}如果${\bf a} = {\bf b}$,这个表达式为零,所以我们应该有$\eta_1 + \eta_2 = 0$,以及$\eta_3 + \eta_4 = 0$。我们接下来需要确定的是它的符号。这个可以代入某个具体的函数进去就可以了。比如我们取${\bf a} = xi$, 以及${\bf b} = yj$,此时只有前面量项会有贡献,我们有$\eta_1=-1$, $\eta_2 + 1$。类似,我们考虑${\bf a} = yi$, 以及${\bf b} = xj$,${\bf a} \times {\bf b} = xy k$, 此时后面两项有贡献,得到$\nabla \times xy k = x i - y j$。右边表达式为$- \eta_3 k \times {\bf b} + \eta_4 k \times {\bf a}$,所以$\eta_3 = -1$,以及$\eta_4 = 1$。最后我们得到\begin{equation*} -(\nabla \cdot {\bf a}) {\bf b} + (\nabla \cdot {\bf b}) {\bf a} - (\nabla \times {\bf a}) \times {\bf b} + (\nabla \times {\bf b}) \times {\bf a}. \end{equation*}我们可以在后面的表中找到这个表达式。
这个问题和电磁学中的磁场有关,比如\begin{equation*} \nabla\times {\bf B} = \nabla \times \nabla \times {\bf A} = \nabla (\nabla \cdot {\bf A} - \nabla^2 {\bf A} = -\nabla^2 {\bf A}. \end{equation*}其中${\bf B}$是磁场,${\bf A}$是磁矢势。这里我们已经利用$\nabla \times \nabla = 0$,所以只有两项,而不是四项。
$\nabla {\bf a}\cdot {\bf b}$,这是一个矢量,它只能由一些矢量来构成,所以我们猜测\begin{equation*}\nabla {\bf a}\cdot {\bf b} = \eta_1 (\nabla \cdot {\bf a}) {\bf b} + \eta_2 (\nabla \cdot {\bf b}) {\bf a} +\eta_3 (\nabla \times {\bf a}) \times {\bf b} + \eta_4 (\nabla \times {\bf b}) \times {\bf a}. \end{equation*} 我们可以用第9条的方法分析这个表达式,并证明所有系数都是$\eta_i = +1$。这是因为$\eta_i = -1$是为了某些极限下让表达式为零,对于对称表达式,没有这个符号问题,所以\begin{equation*}\nabla {\bf a}\cdot {\bf b} = (\nabla \cdot {\bf a}) {\bf b} + (\nabla \cdot {\bf b}) {\bf a} + (\nabla \times {\bf a}) \times {\bf b} + (\nabla \times {\bf b}) \times {\bf a}. \end{equation*}
${\bf a} \times \nabla \times {\bf a}$。我们要利用$\nabla$算子以及${\bf a}$构造一个矢量,只能有$\nabla {\bf a}^2$以及$\nabla \cdot {\bf a} {\bf a}$,所以我们猜测\begin{equation*} {\bf a} \times \nabla \times {\bf a}= \eta_1\nabla {\bf a}^2 + \eta_2 \nabla \cdot {\bf a} {\bf a}. \end{equation*}我们代入一个函数,比如${\bf a} = -y j$,那么${\bf a} \times k = -y i$。右边应该为$2\eta_1 = 1$,所以$\eta_1 = 1/2$。另外,我们选择${\bf a} = xi + yj$,所以有$\eta_2 = -1$,所以我们得到\begin{equation*} {\bf a} \times \nabla \times {\bf a}= {1\over 2} \nabla {\bf a}^2 - \nabla \cdot {\bf a} {\bf a}. \end{equation*}

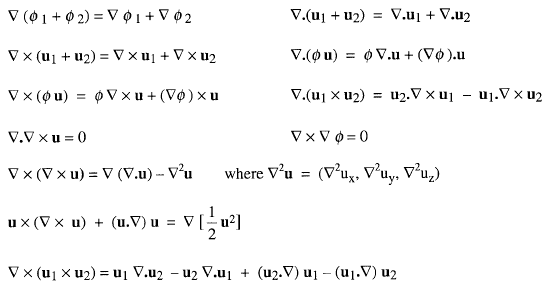
(图片来自网络:Vector Calculus)
有些教材可能会采用Kronecker(克罗内克)函数, 比如${\bf a} \times {\bf b} = \epsilon^{ijk} a_i b_j e_k$,${\bf a} \cdot {\bf b}\times {\bf c} = \epsilon^{ijk} a_i b_j c_k$,以及\begin{equation*} {\bf a}\times {\bf b} \times {\bf c} = \epsilon^{ij\alpha} \epsilon^{\alpha k l} a_i b_j c_k e_l. \end{equation*}这个形式比较数学化,熟悉的人觉得它很漂亮,但需要更好数学技巧,本文不推荐初学者使用这个方法。
总结:在力学中,我们经常需要对矢量做一些计算。本文总结了一些构造的方法,并通过代入特殊表达式来确定其最终的表达式。这个方法是非常有效的。这样做有几个好处。第一、可以免去查表,节省一些时间;第二、可以更好的理解这些公式背后意义。本文希望有助于学生在学习的时候更好掌握它们,也希望任课老师在讲述这些公式的时候可以利用这个构造法来演示其计算过程 --- 至少,不要把它们当作一些复杂的查表公式。有了这个技巧,我们/学生们就不用害怕这些复杂的公式了。
注:欢迎大家转发这篇文章,无须征求我的同意。
https://m.sciencenet.cn/blog-709494-1364231.html
上一篇:《经典力学》札记: 32(速度有关的力)
下一篇:从游泳到独竹漂的力学
全部作者的精选博文
全部作者的其他最新博文
- • 强基的困境
- • 物质和波的最小作用量原理
- • 谈苦与乐
- • 引文中的南郭先生
- • 地球内部的压强有多大?