量子纠缠与最小团覆盖

左芬

上海微观纪元数字科技有限公司

在“量子编码与化学”一文中，我解释了如何用量子编码技术找出分子中的纠缠结构，进而求出近似基态。这回我们来把这一过程跟一个有趣的数学问题联系起来，也就是所谓的“最小团覆盖（minimum clique cover）”。

我们还是以氢气分子H₂为例。不过，这回我们用4个量子比特来表示，并且换一种费米子到玻色子的变换方式，采用Jordan-Wigner变换。在平衡构型附近，变换后的哈密顿量是（d=0.74Å）:

H = - 0.8121706072487122 * IIII

    + 0.1714128264477689 * IIIZ

     - 0.22343153690813486 * IIZI

     + 0.17141282644776892 * IZII

     - 0.22343153690813491 * ZIII

     + 0.12062523483390422 * IIZZ

     + 0.16868898170361207 * IZIZ

     + 0.16592785033770346 * ZIIZ

     + 0.16592785033770346 * IZZI

     + 0.17441287612261597 * ZIZI

     + 0.12062523483390422 * ZZII

      + 0.04530261550379926 * XXYY

      + 0.04530261550379926 * YXXY

      + 0.04530261550379926 * XYYX

       + 0.04530261550379926 * YYXX .

这里I是2*2单位矩阵，X,Y,Z是 Pauli矩阵，量子比特的序号从右到左为0，1,2,3。如果用变分量子电路来逐项计算能量的话，会比较费事，因为每次测量后要重新制备初态。人们想了一个办法，就是把所有这些项（除了平凡项IIII）分成一些由相互对易的算符构成的组。对于每个组来说，只需要做一次态制备和测量，因为它们有共同本征态。具体来说，先根据算符之间两两对易关系画出以下的图：

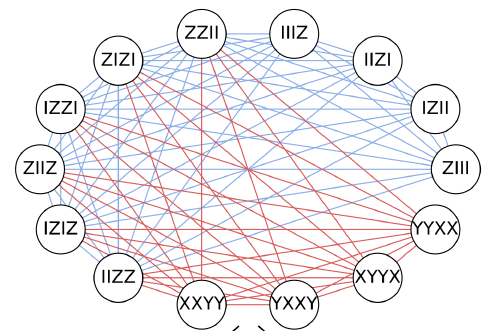
图一：摘自1907.13623。

两个顶点之间有线相连的时候，表示相应的算符对易。这里的蓝线表示每个比特位都对易，而红线表示逐位并不对易，但整体是对易的。后者的一个典型例子就是，两次反对易给出的对易。现在我们需要把这个图分割成一些完全图，也就是团。团的定义要求其中每两个顶点之间都要有边连接，这就保证了其中的算符是两两对易的。同时我们希望团的数目最小，这样态制备和测量的次数最少。于是我们的问题变成了“最小团覆盖”。

可是，最小团覆盖问题是 NP-难的！！！所以，它并不能真的帮我们简化问题。

不过，如果我们有别的办法得到体系的基态，可以反过来求解最小团覆盖问题。而我们最近找到的稳定子近似算法，正好可以做到这一点。对于上面的哈密顿量，我们可以直接读出其相应的稳定子生成元为：

Z₃,  -Z₂,  Z₁,  -Z₀.

对应的态是直积态/Hartree-Fock态|0101>。将图中所有由它们生成的算符放进一个团，再把剩下的算符放进一个团，得到下面的覆盖：

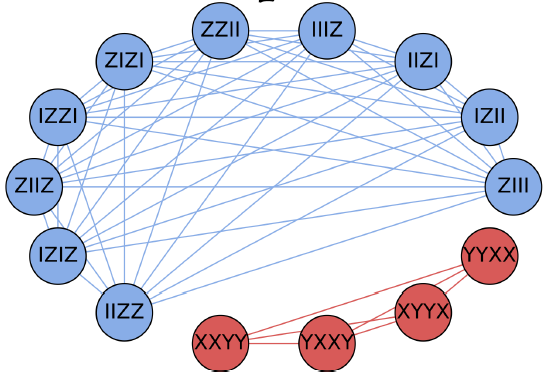
图二：摘自1907.13623。

这一步其实就是用单比特算符来生成多比特算符而已，没什么大不了的。但是下面的结果就不那么一目了然了。

我们考虑远离平衡构型的情况，这时哈密顿量如下（d=2.8Å）:

H = - 0.7340910665455848 * IIII

      + 0.12044907695778825 * ZIIZ

      + 0.12044907695778825 * IZZI

      + 0.12194654795642478 * ZIZI

      + 0.11909854142254998 * IZIZ

       + 0.07326078216819633 * XXYY

       + 0.07326078216819633 * YXXY

       + 0.07326078216819633 * XYYX

       + 0.07326078216819633 * YYXX

      + 0.047527808451266154 * IIIZ

     + 0.03135780838465877 * IIZI

     + 0.04752780845126615 * IZII

     + 0.03135780838465882 * ZIII

     + 0.04718829478959189 * IIZZ

     + 0.04718829478959189 * ZZII.

还是那句话，一定要注意系数大小的变化！此时我们找到的稳定子生成元是：

-Z₃Z₁,  -Z₃Z₀,  -Z₂Z₁,  -X₃X₂Y₁Y₀.

对应的态是纠缠态：

.

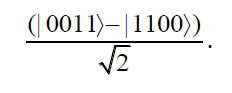
把这些稳定子生成的所有算符放在一起构成团，再把剩下的算符变成团，可以得到：

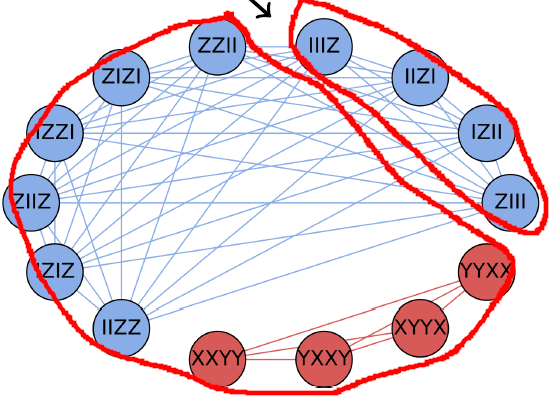
图三：摘自1907.13623。红圈为笔者所加。

我们得到了一个全新的最小团覆盖！这个覆盖并不像之前那样，可以简单推导出来。因为它不仅包含了逐位对易（蓝线），也包含了更一般的对易方式（图一红线，这里被部分省略了）。

于是我们看到，分子体系中不仅存在非平凡的量子纠缠，而且这些纠缠结构还蕴含着复杂的图论问题。而我们之所以能轻松地得到相应的最小团覆盖，是因为大自然巧妙地为图中每个顶点赋予了一定的权重，也就是哈密顿量中的系数。这些系数表现出这样的性质：在最大团中，系数的绝对值都比较大且彼此相近。通过这样的方式，大自然指引着我们找到了答案。让人不得不感叹：造化之神奇，岂是我等凡夫俗子所能想象？