（1）在数学中，有限差分方法（Finite Differenc Methods,FDM），是一种微分方程的数值方法，是通过有限差分来近似导数或者偏导数，从而求得微分方法的近似解。在实际中，许多数学问题都很难得到其解析解，所谓解析解就是可以通过给出解的具体函数形式，从解的表达式中就可以算出任何自变量对应值；而数值解是在特定条件下通过近似计算得出来的一个数值。

举个例子：

一般一元二次方程
a x^2 + b x + c == 0 (a ≠ 0)
的解析解为
x = (- b ±√(b^2 - 4 a c)) / (2 a)
数值解只能由具体的系数确定。

（2）导数的有限差分近似由泰勒展开的推算

假设f(x)在x0处各阶可导，则根据定理，其在x0+h的泰勒展开式为：

{displaystyle f(x_{0}+h)=f(x_{0})+{frac {f'(x_{0})}{1!}}h+{frac {f^{(2)}(x_{0})}{2!}}h^{2}+cdots +{frac {f^{(n)}(x_{0})}{n!}}h^{n}+R_{n}(x),}

其中n!表示是n的階乘，R_n(x)為餘數，表示泰勒多項式和原函數之間的差。可以推導函數f一階導數的近似值：

设定x₀=a，可得：

{displaystyle f(a+h)=f(a)+f'(a)h+R_{1}(x),}

除以h可得：

{displaystyle {f(a+h) over h}={f(a) over h}+f'(a)+{R_{1}(x) over h}}

求解f'(a)：

{displaystyle f'(a)={f(a+h)-f(a) over h}-{R_{1}(x) over h}}

R1(x)是x(x->a时)的高阶无穷小，假设R1(x)很小并可以忽略，可以将"f"的一阶导数近似为：

(一阶近似）

设 n 是一个正整数。如果定义在一个包含 a 的区间上的函数 f 在 a 点处 n+1 次可导，那么对于这个区间上的任意 x，都有：

{displaystyle f(x)=f(a)+{frac {f'(a)}{1!}}(x-a)+{frac {f^{(2)}(a)}{2!}}(x-a)^{2}+cdots +{frac {f^{(n)}(a)}{n!}}(x-a)^{n}+R_{n}(x).}^[2]

其中的多项式称为函数在a 处的泰勒展开式，剩余的{displaystyle R_{n}(x)} 是泰勒公式的余项，是{displaystyle (x-a)^{n}} 的高阶无穷小。

显式方法

热传导方程最常用显式方法的模版

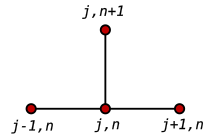
利用在时间{displaystyle t_{n}}的前向差分，以及在位置{displaystyle x_{j}}的二阶中央差分（FTCS 格式），可以得到以下的迭代方程：

{displaystyle {frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}.,}

这是用求解一维导热传导方程的显式方法。

可以用以下的式子求解{displaystyle u_{j}^{n+1}}

{displaystyle u_{j}^{n+1}=(1-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}}

其中{displaystyle r=k/h^{2}.}

因此配合此迭代关系式，已知在时间n的数值，可以求得在时间n+1的数值。{displaystyle u_{0}^{n}}及{displaystyle u_{J}^{n}}的数值可以用边界条件代入，在此例中为0。

此显式方法在{displaystyle rleq 1/2}时，为数值稳定且收敛^[1]。其数值误差和时间间隔成正比，和位置间隔的平方成正比：

{displaystyle Delta u=O(k)+O(h^{2}),}隐式方法

隐式方法的模版

若使用时间{displaystyle t_{n+1}}的后向差分，及位置{displaystyle x_{j}}的二阶中央差分（BTCS 格式），可以得到以下的迭代方程：

{displaystyle {frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}.,}

这是用求解一维导热传导方程的隐式方法。

在求解线性联立方程后可以得到{displaystyle u_{j}^{n+1}}：

{displaystyle (1+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=u_{j}^{n}}

此方法不论{displaystyle r}的大小，都数值稳定且收敛，但在计算量会较显式方法要大，因为每前进一个时间间隔，就需要求解一个联立的数值方程组。其数值误差和时间间隔成正比，和位置间隔的平方成正比：

{displaystyle Delta u=O(k)+O(h^{2}),}

（3） 舍入误差是由于计算机数字限制（四舍五入）引起的

由于计算机的字长有限，进行数值计算的过程中，对计算得到的中间结果数据要使用“四舍五入”或其他规则取近似值，因而使计算过程有误差。这种误差称为舍入误差。在python中输入0.1+0.2，得到的结果是0.30000000000000004，这是舍入误差带来的结果。

There  are  two  approximations  in  numerical  modelling.  One  needs
to  ask  the  questions:  "How  well  is  the  natural  system  modelled  by  the
differential  equations?",  and,  "How  well  is  the  solution  to  the  differential
equations  represented  by  the  computational  algorithm?".  I n   the  analysis
here  more  attention  is  paid  to  the  second  question.  The  first  question
can  only  be  answered  by  studying  the  behaviour  of  the  natural  system
and  comparing  i t   to  the  equations  applied  to  it.  Therefore  i t   will  be
assumed  here  that  the  differential  equations  approximate  the  system  we1 I
despite  the  fact  that  i t   has  been  noticed  that  this  is  not  necessarily
the  case.  Abbott  (1974)  noticed  that  a  difference  scheme  considerably
different  from  the  differential  equations  used  to  describe  a  system,  can
yield  more  accurate  results  than  a  difference  scheme  similar  to  the
differential  equations  when  compared  with  experimental  results.
There  are  three  possible  sources  of  error  associated  with  finite
difference  solutions  to  partial  differential  equations.  I t   is  important
that  one  understands  these  sources,  their  consequence  if  not  control led,
and  means  for  controlling  them.  These  three  sources  of  error  are:
truncation,  discretization,  and  round-off.  Truncation  error  occurs  when
a  derivative  is  replaced  with  a  finite  difference  quotient;  discretization
error  is  due  to  the  replacement  of  a  continuous  model  (function)  with
a  discrete  model;  and  round-off  error  is  essentially  machine  error  in
that  the  algebraic  finite  difference  equations  are  not  always  solved
exactly .

For  finite  difference  solutions  to  be  accurate,  they  must  be  con-
sistent  and  stable.  Consistency  simply  means  that  the  truncation  errors
tend  to  zero  as  Ax  and  At  -  >  0,  i.e.,  as  Ax  and  At  - >  0  the  finite
difference  equation  becomes  the  original  differential  equation.  This  is
examined  i n   the  follcwing  paragraphs.  Stability  implies  the  controlled
growth  of  round-off  error.  Stability  considerations  apply  principally  to
explicit  schemes  to  be  discussed  later.  Any  numerical  scheme  that  allows
the  growth  of  error,  eventually  "swamping"  the  true  solution,  is  unstable.

References

(1) https://zh.wikipedia.org/zh-cn/%E6%9C%89%E9%99%90%E5%B7%AE%E5%88%86%E6%B3%95

(2) https://zh.wikipedia.org/wiki/%E6%B3%B0%E5%8B%92%E5%85%AC%E5%BC%8F

(3) Stephenson, D., kinematic hydrology and modelling. 1986.

(4) Chow, E.A., Applied hydrology. 1988.