对角线证明似乎并不复杂：
 

    假定小数可数，则可将其列为：

 0.a₁₁a₁₂a₁₃...
 0.a₂₁a₂₂a₂₃...
 0.a₃₁a₃₂a₃₃..                                                                      （1）
......
 

其中，a_ij的行标i表示小数个数，列标j表示小数位数。

    在(1)的对角线上，行标等于列标,令

b_ii≠a_ii，（i = 1,2,3.....）    （2）

则康托认为

b=0.b₁₁b₂₂b₃₃....                      （3）

不属于（1），即（1）未能根据假定列出小数(漏了b)，形成矛盾，所以原假定不成立，即小数不可数。

        该证明看上去干净利落，且不乏机智。

    然而，事情真的那么简单吗？

    可数的定义是小数集合与自然数集合一一对应。由（1）可见，与小数一一对应的自然数集合是表示小数个数的行标集合，不是表示小数位数的列标集合。

    这其实是问题的关键。但有的人认为，既然假定小数可数，小数就必须与也是自然数集合的列标集合一一对应。康托在对角线证明其实也是这么做的。这种说法或做法实际上是混淆了行标集合和列标集合：除非能证明行标集合等于列标集合，否则就不允许有这种混淆。以下将会看到，无法严格证明行标集合等于列标集合。

    由于无论是行标集合还是列标集含，都是自然数集合，所以首先必须对自然数集合及其无限性有一个正确的认识。

    任何自然数都是有限的，但是自然数集合却可以是无限的。该简单的事实十分清楚地说明，所谓自然数集合的无限性，是且只能是有限的自然数数值的增加没有上界而已。简单地说，无限即无界。只有这样定义自然数集合的无限性，才不会产生任何悖论，而任何其他定义都会导致矛盾。例如，如果把自然数集合的无限性定义为自然数数值的无限性，就与每个自然数都是有限的这一事实相矛盾。再例如，如果把自然数集合看成是一个静态的，已经完成了的无限集合，就与自然数集合的元素可以通过+1而无限增加这一事实矛盾。

    定义 1 若自然数集合内有限的自然数的增加没有上界，即没有最大自然数，则称该自然数集合是无限的。

    需要指出的是，这个定义已经不是哲学意义上的泛泛而谈，而是能准确描述数学事实的的数学定义。

    定义虽然不需要证明，甚至如何定义在逻辑上也具有一定的自由性:任何能够准确描述事实的定义或定义方法都是可以接受的。但是如果某定义不能准确地描述事实，甚至与所要描述的事实有冲突，这个定义就是没有意义的。

    数列极限中的n→∞，也与定义1相一致: n的增加没有上界。微积分在实践上高度可靠，如果数学分析对无限的认识是错误的，是不可能有这种可靠性的。

    因此，对无限集合，用数学分析加以研究是非常可靠的。

    对于二进制小数，n位小数有m=2ⁿ个小数，用数学分折易证，n→∞时，Lim(m/n)=∞，即用行标表示的小数个数是用列标表示的小数位数的高阶无穷大。因此(1)是一个无限大且无限狭长的长方形矩阵。

     需要特别注意的是，该事实与可数假定并无任何冲突:数学分析只证明了用行标表示的小数个数是用列标表示的小数位数的高阶无穷大，并没有也不可能证明行标不与小数一一对应。

     很多粗心大意的人误以为该事实与可数假定矛盾，显然错了，本质上也是混淆了行标和列标的区别:把小数不能与列标一一对应，误当做小数不能与行标一一对应了。
 

    不过，该事实倒是与基数理论冲突的:在基数理论中，所有的自然数集合都能够一一对应，因此具有相同的基数，而这里的行标集合和列标集合虽然都是自然数集合，都能写成｛1,2,3,....｝,但显然不能一一对应，与基数理论冲突！

    任何理论都不过是用来解释事实的，当理论与事实明显有冲突的时候，我们要做的是对理论进行反思，修改理论使它能够解释事实，而不是反其道而行之：要么对事实视而不见，要么试图通过歪曲事实来维护理论的权威。这些做法都是陡劳的，也是极其严重的错误。
    尤其是某些所谓的理论，甚至连证明都没有，本质上不过是一些猜想或假设，其正确与否更要接受事实的检验而不能反智地对其肓目迷信。

        例如，”各自然数集合可以一一对应，所以具有相同的基数”这一命题本质上不过是一个从未得到，也不可能得到严格证明的假定:如果它可以得到严格证明，就不可能存在任何反例。

        例如上述的长方矩阵的行标和列标都是自然数，但并不能一一对应。

    事实上，无论小数可数还是不可数，无限大的长方形矩阵总是可以存在的。例如，如果(1)表示的是可数的有理小数（其中的有限小数可以补零变成无限小数），行标和列标当然也都是自然数，但两者并不能一一对应而形成正方形矩阵:行标也是列标的高阶无穷大。

 ----------------

         其实，所谓基数理论本身也是康托借鉴了数学分析才得到的。
 

    根据数学分析中的极限定义，极限是有限的确定值，若求出来的极限等于无穷，则通常被认为并不存在极限。

    但任何一个看过康托原著的人都知道，康托把无穷大类比成极限，例如康托说过，→∞与→根号2没有什么两样(大意)，为了便于叙述，不妨将这种极限称为无穷极限以与数学分析中的有限极限相区别。

    康托在没有任何严格数学证明的情况下，想当然地把无穷极限看作与有限极限一样具有确定的数值。然而，容易证明，与有限极限不同，无穷极限并不是一个确定值，而是一个在不断增加的变量：由无穷极限定义中的n→∞时n无上界（定义1）即可看出这一点。同样，康托也在没有任何严格证明的情况下，想当然地认为所有的自然数集合都具有相同的无穷极限。

     这些都充分说明了康托治学态度的不严谨:不但把不可靠的类比推理用到了数学中，混淆了有限极限和无穷极限的区别，而且用想当然代替了严格的数学证明。

     数学是严格的，任何理论都不允许存在哪怕一个反例。

     例如，虽然行标和列标都是自然数集合，它们的无穷极限并不相同:行标集合是列标集合的高阶无穷大。该反例足以推翻康托的想当然论断。

-----------------------.

    既然基数理论不成立，就没有任何理由否认(1)是一个无限大的长方形矩阵这一事实了。也无法证明行标集合等于列标集合，

    另一方面，b=0.b₁₁b₂₂b₃₃….虽然可以无限延长，但其下标对应的行标和列标始终是严格相等的，因此，对角线只考察了小数个数与小数位数严格相同的小数位aii,（i=1,2,3,…），而这些小数位所对应的小数只能形成一个无限大的正方形矩阵，且该正方形矩阵被实际的无限狭长的长方形矩阵所包含。因此，b不在正方形矩阵里面并不意味着b不在（1）所形成的长方形矩阵里，即并没有任何矛盾（见图1）。

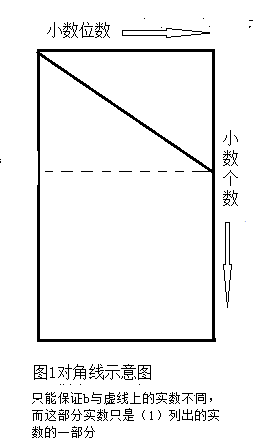
     也就是说，对角线并没有证明实数不可数。

     另外，在康托定理中，如果把自然数集合与二进制小数的位数一一对应，则其各幂集就可与二进制小数一一对应，因此，康托定理也只是证明了小数个数比小数位数多，即(1)是长方形矩阵而已,与小数可数不可数也完全没有关系。

    其实,(1)反而提供了一种证明小数可数的方法:既然小数可以与用自然数表示的行标一一对应且并没有导致任何矛盾，当然就证明了小数是可数的。