首先讲伽利略不变性的意义。 考虑下面的模型，有一个人在静止坐标系，有另外一个人在运动坐标系下看同一个事物(Event): 这个事物可能是某个颜色、某个事故、或者某个物体现状等等。他们看到的会不会是相同的东西? 伽利略不变性是说，物理定律在不同参考下中是不变的。这是非常安全的，否则，如果不同参考下下看到的是不同的事情，那么就有可能时间逆转。这是灾难片才有的故事。

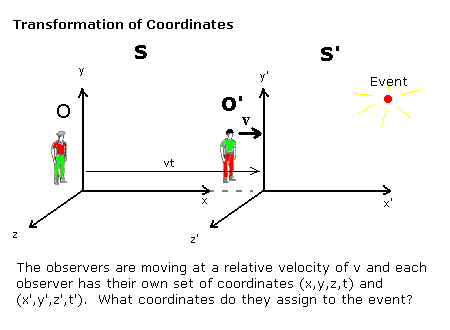
考虑一个一维的情况。我们假设事件是一个波，它有相位

$\psi_O = kx - \omega t$

那么在$O'$参考系下，它的相位应该是不变的(如果相位有明确物理意义，而且是唯一的，量子力学中相位有特殊的含义，不在讨论之内), 那么

$\psi_{O'} =k'x' - \omega' t'$

其中2个参考系的坐标满足下面的关系

$x=x' + vt',  t = t'$

那么我们得到下面的等式

$\omega = \omega' - kv$

其中最后的结果就是Doppler效应。这个问题有趣的是，如果对量子力学又会如何呢? 一般来说，波动力学很难满足伽利略不变性，但是粒子力学却可以。这是一个大问题，以后再讨论。量子力学哈密顿一般都满足伽利略变化不变性，尽管它们都是低能有效模型。哈密顿的伽利略不变性在量子力学中讨论得不多，它在我们量子世界的影响也不是人人都清楚的。一个有趣的问题自然是：如果刘洋在太空中组的是量子力学实验，它会观察到和地球上一样的结果吗？ 我做这样的假设，是因为确实有物理学家在考虑在太空中做实验。

关于能量$\omega=\omega'-kv$很好理解。假设在 $O$参考性下，能量 $E_O = v_o^2/2m$, 那么在$O'$参考性下，能量则为$E_{O'} = (v+v_o)^2/2m$。所以能量必须有一个相应的变化。在量子力学中，能量的这种变化会很有趣。在Maxwell方程中也是如此。