博文
理想气体pVT变化熵变计算的通用公式
|
本文拟介绍理想气体pVT变化熵变计算的三个通用公式,供参考.
理想气体pVT变化熵变计算的通用公式
理想气体pVT变化是常见的热力学过程之一,其熵变计算的通用公式[1]参见如下式(1)、(2)及(3):
ΔS=nCV,mln(T2/T1)+nRln(V2/V1) (1)
ΔS=nCp,mln(T2/T1)-nRln(p2/p1) (2)
ΔS=nCV,mln(p2/p1)+nCp,mln(V2/V1) (3)
计算理想气体pVT变化过程熵变时,需依据具体情况,从式(1)、(2)及(3)选用适合的通用公式.
理想气体pVT变化熵变计算通用公式的应用
2.1 复变过程熵变的计算
复变过程特指经某热力学过程,系统的温度、压强及体积中至少有两个热力学性质发生改变.
例1:1mol的氮气,由298.15K、100kPa的始态,变化至350.15K、60kPa的终态,计算该热力学过程的
熵变.
解:依题氮气为双原子理想气体,Cp,m=7/2R;
选用式(2)计算熵变.
将已知条件代入式(2)可得:
ΔS=nCp,mln(T2/T1)-nRln(p2/p1)
=1mol×7/2×8.314J·mol-1·K-1×ln(350.15K/298.15K) -1mol×8.314J·mol-1·K-1×ln(60kPa/100kPa)
=4.678J·K-1-4.247J·K-1
=0.431J·K-1
2.2 恒压过程熵变计算
例2. 1mol的氮气,由298.15K、100kPa的始态,恒压变化至350.15K的终态,计算该热力学过程的熵变.
解:依题N2的Cp,m=7/2·R
选用式(2)计算熵变.
将已知条件代入式(2)可得:
ΔS=nCp,mln(T2/T1)-nRln(p2/p1)
=1mol×7/2×8.314J·mol-1·K-1×ln(350.15K/298.15K) -1mol×8.314J·mol-1·K-1×ln(100kPa/100kPa)
=4.678J·K-1
2.3 绝热过程熵变计算
例3:1mol的氮气,由298.15K、100kPa的始态,经绝热过程变化至60kPa的终态,计算该热力学过程的
熵变.
解:依题N2的CV,m=5/2·R;Cp,m=7/2·R
对于热力学元熵过程,准静态过程假说[2]认为:
δQ=T·dS (4)
δWV=-p·dV (5)
热力学第一定律表示式参见如下式(6).
dU=T·dS -p·dV+δW' (6)
对于理想气体pVT变化,δW' =0
此时式(6)可化简为:dU=T·dS -p·dV (7)
又因为:dU=nCV,m·dT (8)
将绝热条件及式(8)依次代入式(7)可得:
nCV,m·dT =-p·dV (9)
式(9)变量分离并积分可得:
T·Vγ-1=k1 (10)
将理想气体状态方程代入式(10)可得:
p·Vγ=k2 (11)
Tγ·p1-γ=k3 (12)
式(10)、(11)及(12)可称绝热过程理想气体状态方程.
绝热过程示意参见如下图1.
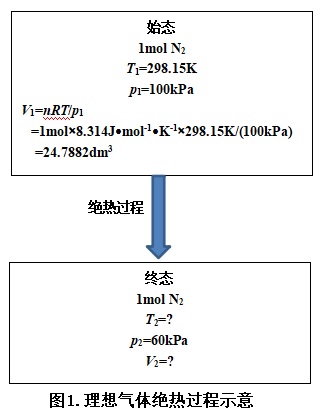
由式(10)、(11)及(12)计算可得:T2=257.7K, V2=35.704dm3
将p1、p2及V1、V2数据分别代入式(3)可得:
ΔS=nCV,mln(p2/p1)+nCp,mln(V2/V1)=1mol×5/2×8.314J·mol-1·K-1·ln(60kPa/100kPa)
+1mol×7/2×8.314J·mol-1·K-1·ln(35.704dm3/24.788dm3)
=-10.617J·mol-1·K-1+10.617J·mol-1·K-1=0
备注:热力学绝热元熵过程,ΔS≡0,与过程是否可逆无关.
3. 结论
理想气体pVT变化熵变计算通用公式包括:
⑴ΔS=nCV,mln(T2/T1)+nRln(V2/V1);
⑵ΔS=nCp,mln(T2/T1)-nRln(p2/p1) ;
⑶ΔS=nCV,mln(p2/p1)+nCp,mln(V2/V1).
参考文献
[1]天津大学物理化学教研室编. 物理化学(上册,第四版).北京:高等教育出版社, 2001,12:119.
[2]余高奇. 热力学第一定律研究.http://blog.sciencenet.cn/u/yugaoqi666. 科学网博客, 2021,8.
https://m.sciencenet.cn/blog-3474471-1359669.html
上一篇:不可逆过程熵变的计算
下一篇:热力学过程的自发性与吕▪查德里原理