博文
《经典力学》札记: 32(速度有关的力)
 精选
精选
|
《经典力学》札记: 32(速度有关的力)
龚明,中国科学技术大学
牛顿力学中,力是势场的梯度,我们有\begin{equation*} {\bf F} = -\partial_{\bf x} U({\bf x}). \end{equation*}日常经验告诉我们,势能是位置的函数,和速度无关,所以力和位置有关,而和速度无关。这个关系对我们理解一些自然现象有非常大的帮助的,如果${\bf F}({\bf x})$和速度无关,那么有伽利略变换不变性。但是我们还是有很多问题,它们的力和速度有关---本文讨论的问题还是在欧几里得坐标系下展开的,如果在广义坐标下研究这个问题,而广义坐标是可以任意选择的,那么力和速度有关就不奇怪了。本文主要总结几个力和速度相关的问题。
1. 阻尼力
阻尼力一般可以写成\begin{equation*} {\bf f} = -\gamma {\bf v}. \end{equation*}这个力可以如此理解,如果它和位置有关,则是抛物势的梯度了,而阻尼力是消耗能量的。因此,它不可能是位置的函数,而只能是速度的函数。它和我们的生活经验也是符合的,阻尼运动的物体是要消耗能量的,一个做阻尼运动的物理最终会静止下来。但要注意,不是所有的消耗能量的过程都和速度有关,比如实验证明,摩擦力$f = \mu N$(高中的主要内容),其中$\mu$为摩擦力系数,它和物理的运动速度无关。
2. 电磁学的Lorentz力
Lorentz力给出\begin{equation*} {\bf f} =e ({\bf E} + {\bf v} \times {\bf B}). \end{equation*}其中, ${\bf E}$为电场,${\bf B}$为磁场,${\bf v}$为带电粒子的运动速度。这个关系对任何速度($v < c$)都是成立的。显然,它不符合伽利略变换不变性。假设在不同的参考系上看这个问题,电场和磁场是一样的,但是它们的速度不同,则力不同。电磁学对它的解释是电场、磁场也要做相应变换。我们看到,磁场的力垂直与速度方向,所以磁场只会导致回旋运动,而不对系统的运动做功。
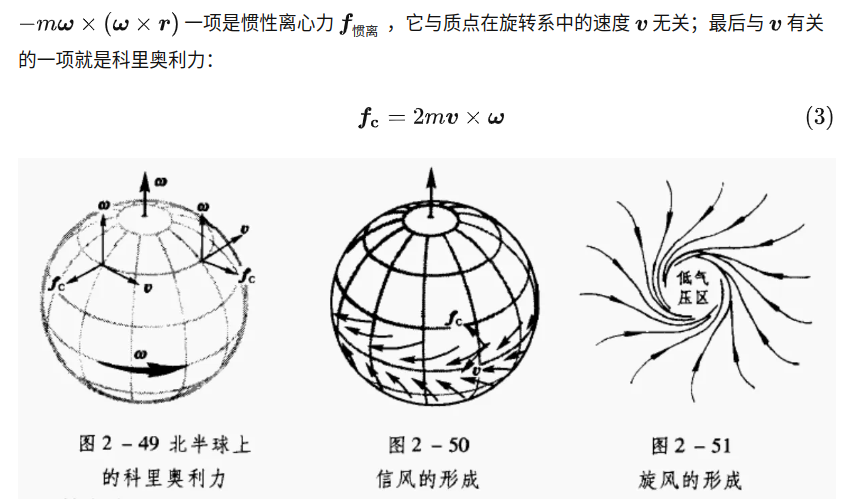
(图片来自网络:https://www.zhihu.com/question/406884475; 离心力和位置有关,而科里奥利力和速度有关。 )
3. 科里奥利力(Coriolis)
假设非惯性参考系$S'$绕着惯性参考系$S$运动,那么$S'$中的任意矢量${\bf A}$,在惯性参考系看其运动满足(即著名的哥氏定理/科里奥利力定理)\begin{equation*} {d {\bf A} \over dt} ={d {\bf A} \over dt }|_{S'} + {\boldsymbol \omega} \times {\bf A}. \end{equation*}这个公式的意义非常明确,在惯性参考系(绝对运动)的运动速度由两个部分构成,即非惯性参考系的相对运动速度加上转动导致的连带运动速度。如果${\bf A} = {\bf r}$,那么我们得到速度\begin{equation*} {\bf v} = {\bf v}' + {\boldsymbol \omega} \times {\bf r}. \end{equation*} 从而可以计算得到加速度\begin{equation*} {\bf a} = {\bf a}' + 2{\boldsymbol \omega} \times {\bf v}' + {d{\boldsymbol \omega} \over dt} \times {\bf r} + {\boldsymbol \omega}\times ({\boldsymbol \omega} \times {\bf r}). \end{equation*} 这个结果里面包括了一个科里奥利力 \begin{equation*} {\bf f}_c = - 2m {\boldsymbol \omega} \times {\bf v}'. \end{equation*} 可以看出来,非惯性系会感受到一个和速度相关的力。尽管这个力是虚构的,为了让物体在非惯性系中运动也有牛顿方程而等价描述的。在经典力学中,我们会讨论在非惯性系统中的有效拉格朗日量,以及对应的拉格朗日方程。所以拉格朗日方程不仅可以在任意广义坐标下写出来,而且可以被推广到非惯性系,即它适用于任意参考系---自然也包括部分学生要涉及到的天体物理和广义相对论等。甚至,我们可以比较电磁场的拉格朗日量以及非惯性系统中的拉格朗日量,并发现它们的类似关系。显然,这两个拉格朗日量有很多相似的地方,比如它们都不满足伽利略变换不变性。
科里奥利力和Lorentz力有许多相似的地方。如果我们将质量替换为电荷,角速度替换为磁场,那么Lorentz力和科里奥利力就可以互换。此外,这些力都和运动方向是垂直的,它们改变了运动方向,但是不对系统做功。对科里奥利力而言,这是显而易见的,因为科里奥利力是一个虚构的力(fictitious force),它只在非惯性系中存在;在惯性系统中就消失了。
速度和力相关,可能导致很多应用。目前有不少物理原理都可以用来测量流量的速度。比如电磁流量计利用法拉第效应,电压为 $U = k v B D$,其中$D$为直径、$B$为磁场强度,$v$为流速,$k$为引入的某个因子。Lorentz力流量计采用的是完全不同的物理原理。类似的,科里奥利力可以用来构造科里奥利力流量计。电磁流量计要求粒子是带电的,科里奥利力流量计则没有这个要求(注意$e$和$m$的对应关系)。当然还有很多其它的流量计,它们都在不同的场合得到了广泛应用。
本文写完后,作者发现下面的网页对Lorentz力和科里奥利力之间的类比关系有一个更加详细的推导和证明(题目为[Physics] Resemblance between Coriolis force and magnetic part of Lorentz force):
(图片来自百度图片,各种不同的科里奥利质量流量计)
科里奥利力现象的应用非常广泛:1)地理学的柏尔定律说的是,在地球上北(南)半球的河流,沿着河流方向右(左)边的何道冲刷更加严重;2)信风在运动过程中会发生偏转; 3)傅科摆可以用来确定地球的自转; 4)质量流量计,以及在石油、天然气等测量方面的应用。这是因为${\bf f} = g m \boldsymbol{\omega} \times {\bf v}' = m {\bf a}$,所以它可以测量质量和流量(包括速度等)。可见,科里奥利力不仅是很多领域的基本概念,它也有很多具体的应用价值。
4. 流体力学中的速度场和加速度场
流体力学中速度场和加速场满足方程\begin{equation*} {\bf a} = {D {\bf u} \over Dt} = {\partial {\bf u} \over \partial t} + {\bf u} \cdot \nabla {\bf u}. \end{equation*}第二部分来自速度场${\bf u}$的空间分布---它也是和速度有关的。如果${\bf u} = \boldsymbol{\omega} \times {\bf r}$,那么${\bf u} \cdot \nabla {\bf u} = \boldsymbol{\omega} \times {\bf u}$,这个表达式和科里奥利力或者电磁力非常相似。如果我们继续取${\bf u} = \boldsymbol{\omega} \times {\bf r}$,则可以得到$\boldsymbol{\omega} \times {\bf u} = -\omega^2 {\bf r}_\perp$。在麦克斯韦方程出来之前,科学家已经做了很多关于矢量力学的计算,其中最重要的可能就是流体力学和固体力学。随着矢量微积分(vector calculus)的发展,以及Stokes定理等的提出,我们对这些问题的描述就更加方便了。
注:大气和流体都有类似旋转问题,目前我们见到的流体力学方程都没有考虑这个效应。对于旋转的流体,比如在一个圆桶中旋转的流体,或者地球表面的大气运动,我们可能需要考虑这个力,即在欧拉流体方程中加入这个力,所以\begin{equation*} {\partial {\bf u} \over \partial t} + {\bf u} \cdot \nabla {\bf u} = -{\nabla P \over \rho} - 2\boldsymbol{\omega}\times {\bf u} + \mu \nabla^2 \boldsymbol{u}. \end{equation*} 其中$P$是压强,$\rho$是密度。尤其是,如果$\boldsymbol{\omega}({\bf x}, t)$和位置有关(类似电磁场中磁场和位置有关),那么它的运动会要复杂得多,也会有趣得多。
总结:本文将几个常见的力和速度的关系拿出来对比和总结。我们看到这个关系在理论物理中有重要应用,而且也导致一些具体的产品。鉴于科里奥利力已经被广泛讨论,本文的科普方面的价值在于将它和几种和速度有关的力放在一起比较,由此可以突显出这种力的独特性。
补充材料:科里奥利(Coriolis, Gustave Gaspard de,1792~1843)法国物理学家。1808年进拿破仑工科学校求学,毕业后在该校任教。1836年当选为法国科学院院士。1838年起在巴黎综合工科学校教授数学物理,并担任业务主任。他是对动能和功给出确切的现代定义的第一个人(1929年),也是第一个提出科里奥利力(1835年)。他的研究多和具体应用问题有关,这可能和当时法国的科学研究环境有关。---基于百度百科总结和整理。
参考文献:
1. 贺宣庆、崔砚生,科里奥利力在流量测量中的应用,物理与工程,2005年。
2. Anders Persson, The Coriolis Effect, Four centuries of conflict between common sense and mathematics, Part I: A history to 188, 2005.
注:欢迎大家转发这篇文章,无须征求我的同意。
https://m.sciencenet.cn/blog-709494-1363845.html
上一篇:《经典力学》札记: 31 (微振动)
下一篇:从游泳到独竹漂的力学
全部作者的精选博文
全部作者的其他最新博文
- • 强基的困境
- • 物质和波的最小作用量原理
- • 谈苦与乐
- • 引文中的南郭先生
- • 地球内部的压强有多大?